Chaos in ocular aberration dynamics of the human eye
- PMID: 22567581
- PMCID: PMC3342193
- DOI: 10.1364/BOE.3.000863
Chaos in ocular aberration dynamics of the human eye
Abstract
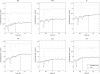
Since the characterization of the eye's monochromatic aberration fluctuations in 2001, the power spectrum has remained the most widely used method for analyzing their dynamics. However, the power spectrum does not capture the complexities of the fluctuations. We measured the monochromatic aberration dynamics of six subjects using a Shack-Hartmann sensor sampling at 21 Hz. We characterized the dynamics using techniques from chaos theory. We found that the attractor embedding dimension for all aberrations, for all subjects, was equal to three. The embedding lag averaged across aberrations and subjects was 0.31 ± 0.07 s. The Lyapunov exponent of the rms wavefront error was positive for each subject, with an average value of 0.44 ± 0.15 µm/s. This indicates that the aberration dynamics are chaotic. Implications for future modeling are discussed.
Keywords: (330.4875) Optics of physiological systems; (330.7326) Visual optics, modeling.
Figures



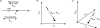



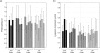

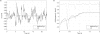

References
LinkOut - more resources
Full Text Sources
