Structural and energetic basis of allostery

Abstract

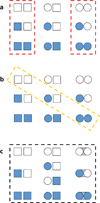
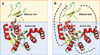
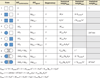
Allostery is a biological phenomenon of fundamental importance in regulation and signaling, and efforts to understand this process have led to the development of numerous models. In spite of individual successes in understanding the structural determinants of allostery in well-documented systems, much less success has been achieved in identifying a set of quantitative and transferable ground rules that provide an understanding of how allostery works. Are there organizing principles that allow us to relate structurally different proteins, or are the determinants of allostery unique to each system? Using an ensemble-based model, we show that allosteric phenomena can be formulated in terms of conformational free energies of the cooperative elements in a protein and the coupling interactions between them. Interestingly, the resulting allosteric ground rules provide a framework to reconcile observations that challenge purely structural models of site-to-site coupling, including (a) allostery in the absence of pathways of structural distortions, (b) allostery in the absence of any structural change, and (c) the ability of allosteric ligands to act as agonists under some circumstances and antagonists under others. The ensemble view of allostery that emerges provides insights into the energetic prerequisites of site-to-site coupling and thus into how allostery works.

Figure 1

Three schematic models of protein allostery. Each panel depicts all possible microstates of the ensemble of a two-domain allosteric protein, perhaps dimeric invertebrate hemoglobin. Each subunit of the protein can adopt two distinct conformations, tensed (squares) or relaxed (circles), and two distinct modes of ligand binding, unbound (open shapes) or bound (filled shapes). Dashed boxes indicate the possible microstates allowed under the postulates of each model. (a) Model of Monod, Wyman, Changeux (MWC). (b) Model of Koshland, Nemethy, Filmer (KNF). (c) The ensemble allosteric model (EAM) presented in this work. Note that the EAM permits a greater number and diversity of allowed microstates and incorporates a finite subunit interaction energy (diagonal-striped area between circular subunits). 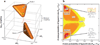The authors believe that these differences endow the EAM with a superior ability to explain, unify, and predict protein allostery. The enumerations of the partition functions corresponding to each of these models are given in Figure 5, and additional details are listed in Table 1.

Figure 2

The structure-based and non-structure-based views of allostery. (a) A hypothetical two-domain protein (blue and orange boxes) contains effector and active sites. The structure-based view of allostery posits that one or a small number of unique pathways of structural deformations (arrows) propagate energy between the sites, thus enabling the allosteric mechanism. Such a view tacitly assumes that the free energy of the allosteric mechanism is proportional to the enthalpy of the noncovalent bonds made and broken along this pathway. (b) A hypothetical two-domain protein (blue and orange boxes) contains effector and active sites. The non-structure-based view of allostery posits that regional changes in dynamics, protein, and/or solvent conformational entropy, or population shifts, are the dominant contributors to the free energy of the allosteric mechanism. Unique energetic pathways are difficult or impossible to place on a single molecular structure of the protein because the free energy is potentially a combination of enthalpic and entropic contributions from many sources.

Figure 3

The ensemble allosteric model (EAM) applied to a two-domain allosteric protein. (a) Schematic representation of a hypothetical two-domain allosteric protein. Domain I (orange box) binds ligand A, and domain II (blue box) binds ligand B. The diagonal-striped area depicts a specific interaction between the two folded domains (i.e., R states) with a free energy Δg_int. Note that this system is conceptually identical to the protein ensemble depicted in Figure 1c. (b) Boltzmann-weighted populations of each microstate in the ensemble. R, relaxed, or high-affinity, state; T, tense, or low-affinity, state. Although the cartoons for T domains appear unstructured, all equations apply equally well to the case in which both T and R states are structured but exhibit a difference in binding affinity. (c) A specific case demonstrating allosteric coupling: Stabilizing domain II with ligand B also stabilizes domain I owing to the favorable interaction energy. Site-to-site coupling is evaluated through the addition of ligand B. Because addition of ligand B stabilizes those states that bind ligand B, the ensemble probabilities are redistributed. Binding of ligand at site B is thus coupled to the transition of domain I from a T state to a R state (possibly but not necessarily folding of domain I) as described in the text. The biologically reasonable values used for this example are ΔG₁ = −0.7 kcal mol⁻¹, ΔG₂ = −2.3 kcal mol⁻¹, Δg_int = +1.6 kcal mol⁻¹, Δg_Lig,B = −3.0 kcal mol⁻¹.

Figure 4

Coupling response (CR) in the ensemble allosteric model EAM: Disorder maximizes allostery. (a) An exhaustive search of parameter space reveals two nodes (orange regions) where coupling is most substantial (CR > 0.10). Node 1 exhibits agonistic behavior, and Node 2 exhibits antagonistic behavior. Red solid lines indicate the origin of the coordinate system, and the yellow star with red dashed lines indicates the approximate parameter combination used to generate the data in Figure 3c. (b) Plot of the probability of R state (high-affinity) domain I ligand A site versus R state (high-affinity) probability of domain II ligand B site. Colors indicate the relative CR upon addition of ligand B (red is strongest response, white is weakest response). Allosteric coupling is maximized if one or both of the domains are substantially disordered, as indicated. Note that Region 1 corresponds to probabilities calculated from the energetic parameters of Node 2 and vice versa.

Figure 5

Allowed microstates and partition functions for three models of allostery. The two-domain protein depicted can be thought of as dimeric hemoglobin, binding the ligand oxygen (x = [O₂]). Columns MWC, KNF, and EAM specify which microstates are allowed in each model, based on the ensembles of Figure 1. L is the MWC equilibrium between unbound tense (T) and relaxed (R) states, c = K_T,MWC/K_R,MWC is the MWC coupling parameter, and K_T,MWC and K_R,MWC are the MWC affinities of the T and R states, respectively, for oxygen. K is the KNF affinity of the R state for oxygen and −RTlnσ represents the KNF-Pauling perturbed interaction energy. K_conf is the EAM equilibrium between unbound T and R states, ϕ_int is the EAM interaction statistical weight, Δg_Lig,T = −RTln(K_Tx), and Δg_Lig,R = −RTln(K_Rx), where K_T and K_R are the intrinsic association constants for the T and R states, respectively. The mathematical expansions described in the main text result in the three partition functions listed at the bottom of the figure. Each partition function is expressed in terms of the variables of the EAM to facilitate direct comparison of each term (Table 1). Note that the EAM permits the maximum degree of freedom in this allosteric system. Abbreviations: EAM, ensemble allosteric model; MWC, Monod-Wyman-Changeux; KNF, Koshland-Nemethy-Filmer.

Figure 6

The ensemble allosteric model applied to a three-domain allosteric protein. (a) Three domains (possibly subdomains) within a single hypothetical molecule. Each domain is specific to a separate ligand, and each subdomain contains an energetic interaction between the two remaining subdomains. As for the two-domain model, each conformational state may be thought of as tense (low affinity) or relaxed (high affinity), which may possibly be related to the folded state of the domain. Thus, microstate 1, where domain I is low affinity and domains II and III are high affinity, is abbreviated TRR. (b) Free energies and Boltzmann-weighted populations of each microstate in the ensemble. Note that this three-domain model is a simple mathematical extension of that developed above.

Figure 7

A specific combination of parameters for the three-domain ensemble allosteric model (EAM) reveals agonist and antagonist properties co-occurring in the same molecule. (a) A specific combination of parameters consistent with agonism-antagonism is indicated by the black circles: Δg₁₂ = 6.8, Δg₂₃ = 4.8, Δg₁₃ = −1.9, ΔG₁ = −6.75, ΔG₂(2) = 0.6, ΔG₂(1) = −4.4, and ΔG₃ = −2.7 (all values in kcal mol⁻¹). The allosteric response is the change in probability of domain III being in the high-affinity R state upon addition of ligand A. Position 1 (black circle at local maximum) exhibits agonistic response to ligand A in the absence of ligand B. Position 2 (black circle at local minimum) exhibits antagonistic response to ligand A in the presence of ligand B. (b) Ensemble microstate energies of the agonistic example, evaluated using Figure 6b and the parameters listed above. Blue bars indicate energy levels in the absence of ligand A (green ovals), and red bars indicate energy levels in the presence of ligand A. (c) Populations of folded domains for the agonistic model in the absence (left) and presence (right) of ligand A. The population of folded domain III rises from 3% to 51%, as indicated. (d) Ensemble microstate energies of the antagonistic example, evaluated using Figure 6b and the parameters listed above. Blue bars indicate energy levels in the absence of ligand A (green ovals), and red bars indicate energy levels in the presence of ligand A. (e) Populations of folded domains for the antagonistic model in the absence (left) and presence (right) of ligand A. The population of high-affinity domain III decreases from 93% to 58%, as indicated.

Figure 8

Exhaustive search of parameter space of the three-domain ensemble allosteric model (EAM) demonstrates four nodes of parameter combinations that exhibit agonism-antagonism. (a) Interaction parameters that exhibit significant agonistic (>35%) and antagonistic (<−35%) responses are depicted in purple. The axes correspond to values of interaction parameters between coupled domains. In contrast, parameters that were sampled and did not exhibit such behavior are depicted in gray. Each of the colored nodes is represented with +/− signs corresponding to the values of Δg₁₂, Δg₂₃, and Δg₁₃; for instance, ++− corresponds to Δg₁₂ > 0, Δg₂₃ > 0, and Δg₁₃ < 0. This result demonstrates that agonism-antagonism in allosteric systems may be a general thermodynamic phenomenon, i.e., stabilities of individual domains and coupling energies between domains need not be biologically rare combinations of values. (b) All possible interaction architectures that lead to allosteric response competitions between coupled domains are depicted. Red indicates an antagonistic redistribution as a result of interaction, and blue indicates an agonistic redistribution. Note: the color of the arrows connecting domains II and III refers to the overall impact of domain III from stabilization of domain I. For example, in the node denoted −−−, stabilization of domain I destabilizes domain II (making the arrow red). However, that destabilization of domain II (because of negative coupling to domain III) has the effect of stabilizing domain III (making the arrow to domain III blue). (c) All possible interaction architectures that do not elicit allosteric response competitions are depicted. The coloring scheme is similar to that in panel b and demonstrates that certain architectures are limited to agonistic responses (+++, −−+) and antagonistic responses (+−−, −+−). As discussed in the text, the case where domains I and III are negatively coupled is contained in the ++− region in panel a.