Linking agent-based models and stochastic models of financial markets

Abstract

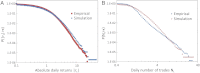
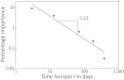
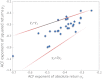
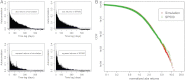
It is well-known that financial asset returns exhibit fat-tailed distributions and long-term memory. These empirical features are the main objectives of modeling efforts using (i) stochastic processes to quantitatively reproduce these features and (ii) agent-based simulations to understand the underlying microscopic interactions. After reviewing selected empirical and theoretical evidence documenting the behavior of traders, we construct an agent-based model to quantitatively demonstrate that "fat" tails in return distributions arise when traders share similar technical trading strategies and decisions. Extending our behavioral model to a stochastic model, we derive and explain a set of quantitative scaling relations of long-term memory from the empirical behavior of individual market participants. Our analysis provides a behavioral interpretation of the long-term memory of absolute and squared price returns: They are directly linked to the way investors evaluate their investments by applying technical strategies at different investment horizons, and this quantitative relationship is in agreement with empirical findings. Our approach provides a possible behavioral explanation for stochastic models for financial systems in general and provides a method to parameterize such models from market data rather than from statistical fitting.

Fig. 1.

Comparison of the distributional properties of simulations with empirical results for the parameter set V_f = 0.4, n₀ = 2¹⁰, b = 1.0. V_f characterizes the how fast one agent’s shares is traded. Empirical data are from the 309 stocks out of S&P 500 index components that have been consistently listed during the 10-y period 1997–2006. There are ≈800,000 data points in empirical data, and 1,000,000 sample points from simulation. (A) Cumulative distributions of daily returns, defined as r_t ≡ log[x_t,close] - log[x_t,open], the difference between the daily opening and closing price of a stock on day t. Thus we ignore overnight returns arising, e.g., due to news events. The price for each stock is normalized to zero mean and unit variance before aggregation into a single distribution. The simulation results agree with the shape of the empirical distribution. The Hill estimator on 1% of tail region gives ξ_r,S&P500 = 3.69 ± 0.07, ξ_r,simulation = 4.08 ± 0.08. (B) The cumulative distribution of the same set of data but analyzed on the daily number of trades. Because the number of trades increases each year, we normalize the data by each stock mean number of trades on a yearly basis before aggregating them into the distributions. The simulation again reproduces the empirical results. The Hill estimator applied to 2.5% of the tail region gives ξ_n,S&P500 = 4.02 ± 0.07, ξ_n,simulation = 4.02 ± 0.08.

Fig. 2.

Plot of survey result (16) on percent importance placed on technical analysis at different time horizons by U.S. fund managers. The plot shows a power-law function with exponent -1.12. We have combined the percent values for both flow and technical analysis at each time horizon, as flow analysis in a broad sense is one type of technical analysis. Technical analysis is heavily used at investment horizons of days to weeks and decays to close to zero at 500 d.

Fig. 3.

Confirmation of the scaling relations Eq. 12. Dependence of γ₁ against γ₂ for the 30 stocks in Dow Jones Indices components. Daily closing prices from 1971–2010 are used for each stock. The two exponents fulfill γ₁ ≤ γ₂ ≤ 2γ₁, so the scaling relation predicted by our stochastic model is consistent with these empirical data. The range of lag, 11 ≤ ℓ ≤ 250, is used because theoretical power-law decay of the ACF is valid for large ℓ, and for ℓ > 250 the ACF values are close to the noise level.

Fig. 4.

Comparison between empirical data and simulation. The empirical data (about 10,000 data points) are from the S&P 500 index daily closing prices in the 40-y period 1971–2010. The simulation are carried out for 50,000 data points to obtain good convergence. Black Monday, October 19, 1989, is removed from the analysis of the ACF. (A) Autocorrelation of simulation vs. S&P 500 index. The simulation results show behavior similar to the S&P 500 for both absolute returns and squared returns. The rate of decay is also similar numerically. (B) The CDF of absolute returns for simulations and the S&P 500. The simulation reproduces the return distribution well.