Games of age-dependent prevention of chronic infections by social distancing

Abstract

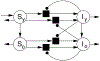
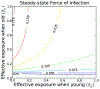
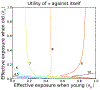
Epidemiological games combine epidemic modelling with game theory to assess strategic choices in response to risks from infectious diseases. In most epidemiological games studied thus-far, the strategies of an individual are represented with a single choice parameter. There are many natural situations where strategies can not be represented by a single dimension, including situations where individuals can change their behavior as they age. To better understand how age-dependent variations in behavior can help individuals deal with infection risks, we study an epidemiological game in an SI model with two life-history stages where social distancing behaviors that reduce exposure rates are age-dependent. When considering a special case of the general model, we show that there is a unique Nash equilibrium when the infection pressure is a monotone function of aggregate exposure rates, but non-monotone effects can appear even in our special case. The non-monotone effects sometimes result in three Nash equilibria, two of which have local invasion potential simultaneously. Returning to a general case, we also describe a game with continuous age-structure using partial-differential equations, numerically identify some Nash equilibria, and conjecture about uniqueness.

Fig. 1

This hypergraph represents the reaction network of System (1). Arrows indicate mass flow, while lines ending in discs identify catalytic interactions.

Fig. 2

The infection pressure $\tilde{\lambda }$, as shown in this contour plot, depends on the components of the aggregate strategy $\overline{\sigma }$ for parameter values given in Eq. (23). The infection pressure is not always monotone increasing in $\overline{\sigma }$. The age-dependent transmission rate interacts with the shortened lifespan, such that the infection pressure is maximized by minimizing the effective exposure of the young.

Fig. 3

Contour plots of the utility $\mathcal{U}(\overline{\sigma },\tilde{\lambda }(\overline{\sigma }))$ as it depends on the aggregate strategy $\overline{\sigma }$. Corresponding infection pressures are shown in Fig. 2. The utility is maximized when the old age-group invests sufficiently to induce herd-immunity, while the young invest nothing. Parameter values given in (Eq. 23).

Fig. 4

Here (left), we show a plot of the solutions of Eq. (21) as c_io is varied. Except for the narrow region when c_io ∈ [.46, .61], there is a unique solution of Eq. (21) corresponding to a unique Nash equilibrium, (right) An illustrative plot of the inclusion relation given by Eq. (21) when c_io = 0.58. The three intersection points determine three infection pressures corresponding to Nash equilibria. The three Nash equilibria corresponding to the solutions of Eq. (21) and along with their infection pressures are $\left({\sigma }^{*},\tilde{\lambda }\right)\in \{(\langle 1,1\rangle ,0.110),(\langle 0.47,1\rangle ,0.13),(\langle 0,1\rangle ,0.18)\}$.

Fig. 5

Contour plots of response utility (top row) and relative invasion potentials (bottom row) of the three candidate equilibria identified in Figure 4(left). The equilibria locations are marked by the black dots. All three are global Nash equilibria because no individual strategy has a relative utility greater than 1 when played against the candidate (top row). The Nash equilibrium 〈.5, 1〉 is a weak equilibrium, as other strategies have relative utility equal to 1 when played against 〈.5, 1〉. The other two are strong equilibria. None of the three Nash equilibria has global invasion potential, as 〈0, 1〉 can not invade 〈1, 1〉, 〈1, 1〉 can not invade 〈0, 1〉, and 〈.5, 1〉 can invade neither of the other two. None of these equilibria correspond to the optimal community behavior (see Figure 3), and in fact, 〈0, 1〉 maximizes the infection pressure. Parameter values given in (Eq. 23).

Fig. 6

Regions of game equilibrium social distancing and the associated values of the susceptible and infected states when the conditional life-expectancy under infection is u_I = 1, c_p = 0.1, ζ = 0.1 (A), u_I = 0.5, c_p = 0.1, ζ = 0.1 (B), and u_I = 0.5, c_p = 0.1, ζ = 0.03 (C). The red regions represent the ages during which social-distancing is optimal, while the intersections of the V_S (black) and Switch (green) curves identify the boundaries of the ages of social distancing. Comparing plots (A) and (B), we see that disability-costs associated with infection have little effect on the equilibrium behavior, despite significant reducing the well-being of infected individuals. Comparing plots (B) and (C), we see that a 3-fold reduction in the disease mortality rate (while β is reduced 3-fold to keep R₀ = 5) reduces the duration of social-distancing from 50 years to 30 years. Thus death seems to be having a greater impact on equilibrium behavior than disability.