Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2012 Jun 1;47(5):506-520.
doi: 10.1016/j.ijnonlinmec.2011.09.025. Epub 2011 Sep 22.

Modeling and numerical simulation of blood flow using the Theory of Interacting Continua

Mehrdad Massoudi  1 , Jeongho Kim, James F Antaki
Affiliations

Modeling and numerical simulation of blood flow using the Theory of Interacting Continua

Mehrdad Massoudi et al. Int J Non Linear Mech. .

Abstract

In this paper we use a modified form of the mixture theory developed by Massoudi and Rajagopal to study the blood flow in a simple geometry, namely flow between two plates. The blood is assumed to behave as a two-component mixture comprised of plasma and red blood cells (RBCs). The plasma is assumed to behave as a viscous fluid whereas the RBCs are given a granular-like structure where the viscosity also depends on the shear-rate.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Shear thinning model for viscosity of RBC phase, calibrated to experimental data of Chien et al (1966) (Chien, Usami et al. 1966) for 90% Ht.
Figure 2
Figure 2
Flow between parallel plates located at Y=−1 and Y=1.
Figure 3
Figure 3
Effect of Reynolds number (Re) on the plasma velocity (left) and the RBC velocity (right)
Figure 4
Figure 4
Effect of Reynolds number (Re) on the volume fraction of RBCs
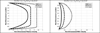
Figure 5
Figure 5
Effect of average volume fraction (N) on the plasma velocity (left) and the RBC velocity (right), without shear-thinning
Figure 6
Figure 6
Effect of average volume fraction (N) on the plasma velocity (left) and the RBC velocity (right) with shear-thinning
Figure 7
Figure 7
Effect of average volume fraction (N) on the volume fraction of RBCs without a shear-thinning (left) and with a shear-thinning (right)
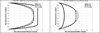
Figure 8
Figure 8
Effect of the material constant (κ) on the plasma velocity (left) and the RBC velocity (right).
Figure 9
Figure 9
Effect of the material constant (κ) on the mean velocity of the mixture and the volume fraction of RBCs
Figure 10
Figure 10
Effect of B31 on the mixture velocity (left) and the volume fraction of RBCs (right).
Figure 11
Figure 11
Effect of B32 on the mixture velocity (left) and the volume fraction of RBCs (right).
Figure 12
Figure 12
Effect of dimensionless gravity (G1) on the plasma and RBC velocity profiles (left) and the volume fraction of RBCs (right)
Figure 13
Figure 13
Effect of combination of dimensionless gravity and shear lift on plasma and RBC velocity profile (left) and the volume fraction of RBCs (right)
Figure 14
Figure 14
Effect of lift coefficient (C3) on the plasma and RBC velocities (left) and the volume fraction of RBCs (right)
Figure 15
Figure 15
Effect of lift coefficient (C3) on the plasma and RBC velocities (left) and the volume fraction of RBCs (right)
Figure 16
Figure 16
Effect of density gradient coefficient (C1) on the plasma velocity (left) and the RBC velocity (right).
Figure 17
Figure 17
Effect of density gradient coefficient (C1) on the volume fraction of RBCs
Figure 18
Figure 18
Effect of drag coefficient (C2) on the plasma velocity (left) and the RBC velocity (right)
Figure 19
Figure 19
Effect of drag coefficient (C2) on the volume fraction of RBCs
Figure 20
Figure 20
Effect of lift coefficient (C3) on the plasma velocity (left) and the RBC velocity (right)
Figure 21
Figure 21
Effect of lift coefficient (C3) on the volume fraction of RBCs
Figure 22
Figure 22
Effect of lift coefficient (C3) on the plasma velocity (left) and the RBC velocity (right)
Figure 23
Figure 23
Effect of lift coefficient (C3) on the volume fraction of RBCs
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Aarts P, Vandenbroek SAT, et al. Blood-platelets are concentrated near the wall and red blood-cells, in the center in flowing blood. Arteriosclerosis. 1988;8(6):819–824. - PubMed
    1. Adkins JE. Non-Linear Diffusion, 1. Diffusion and Flow of Mixtures of Fluids. Phil. Trans. Roy. Soc. London A. 1963;255:607–633.
    1. Adkins JE. Non-Linear Diffusion, 2. Constitutive Equations for Mixtures of Isotropic Fluids. Phil. Trans. Roy. Soc. London A. 1963;255:635–648.
    1. Anderson TB, Jackson R. A fluid mechanical description of fluidized beds. Industrial & Engineering Chemistry Fundamentals. 1967;6(4) 527-&.
    1. Araujo RP, Mcelwain DLS. A mixture theory for the genesis of residual stresses in growing tissues I. Siam Journal on Applied Mathematics. 2005;65 1261-

LinkOut - more resources