Inferring biochemical reaction pathways: the case of the gemcitabine pharmacokinetics

Abstract

Background: The representation of a biochemical system as a network is the precursor of any mathematical model of the processes driving the dynamics of that system. Pharmacokinetics uses mathematical models to describe the interactions between drug, and drug metabolites and targets and through the simulation of these models predicts drug levels and/or dynamic behaviors of drug entities in the body. Therefore, the development of computational techniques for inferring the interaction network of the drug entities and its kinetic parameters from observational data is raising great interest in the scientific community of pharmacologists. In fact, the network inference is a set of mathematical procedures deducing the structure of a model from the experimental data associated to the nodes of the network of interactions. In this paper, we deal with the inference of a pharmacokinetic network from the concentrations of the drug and its metabolites observed at discrete time points.

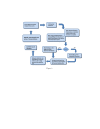
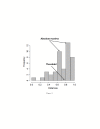
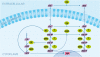
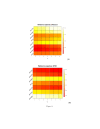
Results: The method of network inference presented in this paper is inspired by the theory of time-lagged correlation inference with regard to the deduction of the interaction network, and on a maximum likelihood approach with regard to the estimation of the kinetic parameters of the network. Both network inference and parameter estimation have been designed specifically to identify systems of biotransformations, at the biochemical level, from noisy time-resolved experimental data. We use our inference method to deduce the metabolic pathway of the gemcitabine. The inputs to our inference algorithm are the experimental time series of the concentration of gemcitabine and its metabolites. The output is the set of reactions of the metabolic network of the gemcitabine.

Conclusions: Time-lagged correlation based inference pairs up to a probabilistic model of parameter inference from metabolites time series allows the identification of the microscopic pharmacokinetics and pharmacodynamics of a drug with a minimal a priori knowledge. In fact, the inference model presented in this paper is completely unsupervised. It takes as input the time series of the concetrations of the parent drug and its metabolites. The method, applied to the case study of the gemcitabine pharmacokinetics, shows good accuracy and sensitivity.

Figure 1

Scheme of the main steps of the network identification method.

Figure 2

Example of histogram of distances between chemical species. It is used to determine a threshold under which an edge is drawn between two species. In this figure, the value of the threshold is 0.75.

Figure 3

Biotransformations and pharmacologic actions of dFdC and its metabolite as reported in a recent study of Veltkamp et al. [[8]].

Figure 4

Experimental concentration profiles of dFdC and dFdU metabolites [[8]]. Concentrations are expressed in nM/L and time is expressed in hours. (A) Time behaviour of extra-cellular and intra-cellular concentration of dFdC; (B) Time behaviour of phosphorylated metabolites of dFdC; (C) Time behavior of intra-cellular concentration of dFdU; (D) time behaviour of phosphorylated metabolites of dFdU.

Figure 5

(A) Bi-dimensional and three-dimensional (B) wiring diagram obtained with a Kruskal-Shepard multidimensional scaling algorithm from real time series of metabolites concentration.

Figure 6

Heatmap representation of the time-lagged correlations between species obtained from measured time series of metabolites concentration.(A) Reference species is the extra-cellular dFdC; (B) Reference species is the intracellular dFdC. On the x-axis, the values of the delay τ are reported.

Figure 7

Heatmap representation of the time-lagged correlations between species obtained from measured time series of metabolites concentration.(A) Reference species is the mono-phosphate metabolite of dFdC. (B) Reference species is the di-phosphate metabolite of dFdC. (C) Reference species is the tri-phosphate metabolite of dFdC. On the x-axis, the values of the delay τ are reported.

Figure 8

Heatmap representation of the time-lagged correlations between species obtained from measured time series of metabolites concentration.(A) Reference species is the intra-cellular of dFdU. (B) Reference species is the di-phosphate metabolite of dFdU. (C) Reference species is the di-phosphate metabolite of dFdU. On the x-axis, the values of the delay τ are reported.

Figure 9

Simulated time behaviour of parent drug and its metabolites. The curves have ben obtained by simulating a mass action model of the interactions depicted in the cartoon of Figure 2. A level of noise equal to the 7% of the concentration values has been artificially introduced to simulate the presence of experimental uncertainties. In this model we asssumed that both the intra- and the intra-cellular concetration of dFdU reach the equilibrium within the first four hours. (A) Time behaviour of extra- and intra-cellular concentrations of dFdC. (B) Time behaviour of the concentrations of phisphorylated metabolites of dFdC. (C) Time behaviour of the concentrations of phisphorylated metabolites of dFdU.

Figure 10

(A) Bi-dimensional and three-dimensional (B) wiring diagram obtained with a Kruskal-Shepard multidimensional scaling algorithm from synthetic time series of metabolites concentration.

Figure 11

Heatmap representation of the time-lagged correlations between species obtained from synthetic time series of metabolites concentration.(A) Reference species is the extra-cellular dFdC; (B) Reference species is the intracellular dFdC. On the x-axis, the values of the delay τ are reported.

Figure 12

Heatmap representation of the time-lagged correlations between species obtained from synthetic time series of metabolites concentration.(A) Reference species is the mono-phosphate metabolite of dFdC. (B) Reference species is the di-phosphate metabolite of dFdC. (C) Reference species is the tri-phosphate metabolite of dFdC. On the x-axis, the values of the delay τ are reported.

Figure 13

Heatmap representation of the time-lagged correlations between species obtained from synthetic time series of metabolites concentration.(A) Reference species is the intra-cellular of dFdU. (B) Reference species is the intracellular dFdU. (C) Reference species is the mono-phosphate metabolite of dFdU. On the x-axis, the values of the delay τ are reported.

Figure 14

(A) Pathway connecting dFdCDP and the intra-cellular concentration of dFdU (dotted arrows).(B) The interaction between dFdUout and dFdC is mediated by the pathway illustrated in this figure. Therefore the reaction R10 (see Table 5) is a false positive inferred reaction.