Analysis of stability and bifurcations of fixed points and periodic solutions of a lumped model of neocortex with two delays

Abstract

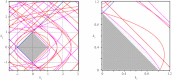
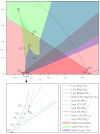
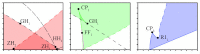
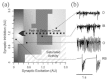
A lumped model of neural activity in neocortex is studied to identify regions of multi-stability of both steady states and periodic solutions. Presence of both steady states and periodic solutions is considered to correspond with epileptogenesis. The model, which consists of two delay differential equations with two fixed time lags is mainly studied for its dependency on varying connection strength between populations. Equilibria are identified, and using linear stability analysis, all transitions are determined under which both trivial and non-trivial fixed points lose stability. Periodic solutions arising at some of these bifurcations are numerically studied with a two-parameter bifurcation analysis.

Fig. 1

Overview of the model. Two cortical layers (red and blue) with excitatory pyramidal cells are connected mutually. The inhibition of the interneurons (green) is modeled intrinsically.

Fig. 2

Bifurcation curves in the $(k_1,k_2)$-plane. ${\tau }_1=11.6$ and ${\tau }_2=20.3$. The right plot shows a detail of the first quadrant only. Blue shows the conditions for fold or transcritical bifurcations (Equations 14a and 14b) and red and magenta depict Hopf bifurcations; equations ${\mathbf{h}}_{+}$ and ${\mathbf{h}}_{-}$, respectively. The gray area represents the stability region as in Corollary 4. The full stability region is hatched in the right diagram.

Fig. 3

Detail of bifurcations. Similar to Figure 2 but now showing the fine structure of branches bounding the stability region. The points ZH and HH correspond with the fold-Hopf and Hopf-Hopf bifurcations from Equations 22 and 23. For clarity, we do not show the stability region. Blue, fold/transcritical; red, asymmetric Hopf; magenta, symmetric Hopf.

Fig. 4

Bifurcations in one parameter. The top shows the bifurcation diagram in ${\alpha }_2$. Different colors represent different solutions, and a thick/thinline indicates that such a solution is stable/unstable. The four diagrams at the bottom show details of the four marked regions in the top diagram. ${\tau }_1=11.6$, ${\tau }_2=20.3$, ${\alpha }_1=0.069$, ${\beta }_1=2$, ${\beta }_2=1.2$.

Fig. 5

Mapping to $(k_1,k_2)$-plane. The curves $E_T({\alpha }_2)$ and $E_N({\alpha }_2)$ show the parametrization of the origin (trivial fixed point) and non-trivial fixed points, respectively, for fixed ${\alpha }_1$. This figure illustrates how some solution branches can regain stability after encountering numerous bifurcations. Blue, fold/transcritical; red, asymmetric Hopf; magenta, symmetric periodic solution; black, parametrization of fixed points.

Fig. 6

Time series in multi-stable regime. Time series of the system for ${\alpha }_2=0.55$, other parameters as in Figure 4 and initial conditions given by Equations 30a, 30b, 30c and 30d. Solid and dashed lines correspond with $x_1$ and $x_2$. Solutions of all four stable branches are obtained: (A) trivial steady state, (B) non-trivial steady state, (C) symmetric periodic solutions and (D) asymmetric periodic solutions. Colors of these time series correspond with the branches in Figure 4.

Fig. 7

Bifurcations in two parameters. Bifurcation diagram in ${\alpha }_1$ and ${\alpha }_2$. Colored regions mark stability regions of indicated solutions. Overlapping areas, depicted with mixed colors, correspond with multi-stability. See text for a description of the points. Stability regions for individual solutions are shown in Figure 8 for clarity.

Fig. 8

Regions of multi-stability. Identical to Figure 7, but showing the stability regions of each type of solution separately. Two partially overlapping ‘triangles’ corresponding with stability of fixed points (left), stability region for symmetric periodic solutions with a small area of bistability caused by cusp point ${\mathit{CP}}_1$ (middle), and region in parameter space where stable asymmetric periodic solutions exist (right).

Fig. 9

Behavior of a detailed network. This figure, copied with permission from [4], shows the behavioral changes of a large physiologically detailed model of neocortex. For varying strengths of excitatory and inhibitory connections, the model’s behavior is classified in one of five categories. See text for a description of the network states and their correspondence to the population model.