Anomalously weak solar convection
- PMID: 22665774
- PMCID: PMC3409726
- DOI: 10.1073/pnas.1206570109
Anomalously weak solar convection
Abstract
Convection in the solar interior is thought to comprise structures on a spectrum of scales. This conclusion emerges from phenomenological studies and numerical simulations, though neither covers the proper range of dynamical parameters of solar convection. Here, we analyze observations of the wavefield in the solar photosphere using techniques of time-distance helioseismology to image flows in the solar interior. We downsample and synthesize 900 billion wavefield observations to produce 3 billion cross-correlations, which we average and fit, measuring 5 million wave travel times. Using these travel times, we deduce the underlying flow systems and study their statistics to bound convective velocity magnitudes in the solar interior, as a function of depth and spherical-harmonic degree ℓ. Within the wavenumber band ℓ < 60, convective velocities are 20-100 times weaker than current theoretical estimates. This constraint suggests the prevalence of a different paradigm of turbulence from that predicted by existing models, prompting the question: what mechanism transports the heat flux of a solar luminosity outwards? Advection is dominated by Coriolis forces for wavenumbers ℓ < 60, with Rossby numbers smaller than approximately 10(-2) at r/R([symbol: see text]) = 0.96, suggesting that the Sun may be a much faster rotator than previously thought, and that large-scale convection may be quasi-geostrophic. The fact that isorotation contours in the Sun are not coaligned with the axis of rotation suggests the presence of a latitudinal entropy gradient.
Conflict of interest statement
The authors declare no conflict of interest.
Figures



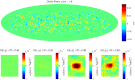

 , r = 0.92, 0.96 R⊙. Interior convection appears to be strongly geostrophically balanced (i.e., rotationally dominated) on these scales. By construction, these measurements are sensitive to lateral flows i.e., longitudinal and latitudinal at these specific depths (r/R⊙ = 0.92, 0.96) and consequently, we denote these flow components (longitudinal or latitudinal) by scalars.
, r = 0.92, 0.96 R⊙. Interior convection appears to be strongly geostrophically balanced (i.e., rotationally dominated) on these scales. By construction, these measurements are sensitive to lateral flows i.e., longitudinal and latitudinal at these specific depths (r/R⊙ = 0.92, 0.96) and consequently, we denote these flow components (longitudinal or latitudinal) by scalars.Comment in
-
Helioseismology challenges models of solar convection.Proc Natl Acad Sci U S A. 2012 Jul 24;109(30):11896-7. doi: 10.1073/pnas.1208875109. Epub 2012 Jul 18. Proc Natl Acad Sci U S A. 2012. PMID: 22814376 Free PMC article. No abstract available.
References
-
- Stein RF, Nordlund Å. Realistic solar convection simulations. Sol Phys. 2000;192:91–108.
-
- Vögler A, et al. Simulations of magneto-convection in the solar photosphere. Equations, methods, and results of the MURaM code. Astron Astrophys. 2005;429:335–351.
-
- Rast MP. Compressible plume dynamics and stability. J Fluid Mech. 1998;369:125–149.
-
- Miesch MS. Large-scale dynamics of the convection zone and tachocline. Living Reviews in Solar Physics. 2005;2:1–139.
-
- Weiss A, Hillebrandt W, Thomas H, Ritter H. Cox and Giuli’s Principles of Stellar Structure. Second edition. Cambridge, UK: Princeton Publishing Associates; 2004.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

