A tale of many cities: universal patterns in human urban mobility
- PMID: 22666339
- PMCID: PMC3362592
- DOI: 10.1371/journal.pone.0037027
A tale of many cities: universal patterns in human urban mobility
Erratum in
- PLoS One. 2012;7(9). doi:10.1371/annotation/ca85bf7a-7922-47d5-8bfb-bcdf25af8c72
Abstract
The advent of geographic online social networks such as Foursquare, where users voluntarily signal their current location, opens the door to powerful studies on human movement. In particular the fine granularity of the location data, with GPS accuracy down to 10 meters, and the worldwide scale of Foursquare adoption are unprecedented. In this paper we study urban mobility patterns of people in several metropolitan cities around the globe by analyzing a large set of Foursquare users. Surprisingly, while there are variations in human movement in different cities, our analysis shows that those are predominantly due to different distributions of places across different urban environments. Moreover, a universal law for human mobility is identified, which isolates as a key component the rank-distance, factoring in the number of places between origin and destination, rather than pure physical distance, as considered in some previous works. Building on our findings, we also show how a rank-based movement model accurately captures real human movements in different cities.
Conflict of interest statement
Figures

 and a threshold
and a threshold  confirming previous works on human mobility data. The spatial granularity offered by GPS data allows for the inspection of human movements at very small distances, whereas the global reach of Foursquare reveals the full tail of the planetary distribution of human movements.
confirming previous works on human mobility data. The spatial granularity offered by GPS data allows for the inspection of human movements at very small distances, whereas the global reach of Foursquare reveals the full tail of the planetary distribution of human movements.
 ,
,  ) suggests that the distribution of intracity displacements can not be fully described by a power law. Short transitions which correspond to a large portion of the movements distribution are not captured by such process.
) suggests that the distribution of intracity displacements can not be fully described by a power law. Short transitions which correspond to a large portion of the movements distribution are not captured by such process.

 ). A longer mean transition corresponds to the expectation of a sparser urban environment, indicating that the number of available places per area unit could have an impact on human urban travel.
). A longer mean transition corresponds to the expectation of a sparser urban environment, indicating that the number of available places per area unit could have an impact on human urban travel.
 ). To measure the area of a city we have segmented the spatial plane around its geographic midpoint in squares of size
). To measure the area of a city we have segmented the spatial plane around its geographic midpoint in squares of size 
 . The area of a city has been defined as the sum area of all squares that feature at least five places.
. The area of a city has been defined as the sum area of all squares that feature at least five places.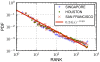
 and
and  , we measure
, we measure  defined as the number of places that are geographically closer to
defined as the number of places that are geographically closer to  than
than  . We observe that the distributions of the three cities collapse to a single line, which suggests that universal laws can be formulated in terms of the rank variable. The observation confirms the hypothesis that human movements are driven by the density of the geographic environment rather than the exact distance cost of our travels. A least squares fit (red line) underlines the decreasing trend of the probability of a jump as the rank of a places increases.
. We observe that the distributions of the three cities collapse to a single line, which suggests that universal laws can be formulated in terms of the rank variable. The observation confirms the hypothesis that human movements are driven by the density of the geographic environment rather than the exact distance cost of our travels. A least squares fit (red line) underlines the decreasing trend of the probability of a jump as the rank of a places increases.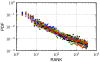

 to a place
to a place  in a city, only depends on the rank value of
in a city, only depends on the rank value of  with respect to
with respect to  . In the case of the gravity model, the deterrence affect of distance is co-integrated with a mass based attractiveness of a place
. In the case of the gravity model, the deterrence affect of distance is co-integrated with a mass based attractiveness of a place  . The associated mass,
. The associated mass,  , has been defined according to the number of neighboring places. The parameters for the depicted fit of the gravity model are
, has been defined according to the number of neighboring places. The parameters for the depicted fit of the gravity model are  and
and  meters. The places of a city employed for the simulation experiments where those observed in the Foursquare dataset, hence while the rank-based model is the same for all cities the underlying spatial distribution of places may vary. Excellent fits are observed for all cities analyzed. It is interesting to note that the model is able to reproduce even minor anomalies, such as the case of San Francisco where we have ‘jumps’ in the probability of a movement at 20 and 40 kilometers.
meters. The places of a city employed for the simulation experiments where those observed in the Foursquare dataset, hence while the rank-based model is the same for all cities the underlying spatial distribution of places may vary. Excellent fits are observed for all cities analyzed. It is interesting to note that the model is able to reproduce even minor anomalies, such as the case of San Francisco where we have ‘jumps’ in the probability of a movement at 20 and 40 kilometers.
 and
and  meters, whereas in the case of the rank-distance model an exponent
meters, whereas in the case of the rank-distance model an exponent  has been used to simulate movement in all cities and corresponds to the empirical average of the exponents resulting from the fit of the rank value distributions.
has been used to simulate movement in all cities and corresponds to the empirical average of the exponents resulting from the fit of the rank value distributions.
 and
and  .
.
 in a city. We have enumerated 11808, 15970, 15617 unique venues for Houston, San Francisco and Singapore respectively. The probability is increasing with
in a city. We have enumerated 11808, 15970, 15617 unique venues for Houston, San Francisco and Singapore respectively. The probability is increasing with  , as expected in two dimensions before falling due to finite size effect. It is interesting to note that the probability for two randomly selected places to be the origin and destination of a jump monotonically decreases with distance (see SI).
, as expected in two dimensions before falling due to finite size effect. It is interesting to note that the probability for two randomly selected places to be the origin and destination of a jump monotonically decreases with distance (see SI).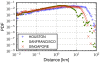
 , between the empirically observed distribution of displacements in a city
, between the empirically observed distribution of displacements in a city  and
and  which is the one obtained by the rank-distance model. On the x-axis the probability of randomization,
which is the one obtained by the rank-distance model. On the x-axis the probability of randomization,  , is depicted. In order to randomize the spatial distribution of places in a city, we iterate through the associated set of places
, is depicted. In order to randomize the spatial distribution of places in a city, we iterate through the associated set of places  and the coordinates of a place
and the coordinates of a place  ,
,  are randomized with probability
are randomized with probability  . A new pair of coordinates,
. A new pair of coordinates,  , is assigned uniformly and within a pre-specified range, where
, is assigned uniformly and within a pre-specified range, where 
 and
and 
 .
.  corresponds to the case that the original distribution of displacements within a city is maintained, whereas the opposite extreme where
corresponds to the case that the original distribution of displacements within a city is maintained, whereas the opposite extreme where  equals
equals  means that all places have been randomized. The errors bars correspond to standard deviations across cities.
means that all places have been randomized. The errors bars correspond to standard deviations across cities.References
-
- Ravenstein EG. The laws of migration. 1885;48:167–235.
-
- Zheng Y, Zhang L, Xie X, Ma WY. Mining interesting locations and travel sequences from gps trajectories. 2009. In: Proceedings of WWW' 09.
-
- Zheng VW, Zheng Y, Xie X, Yang Q. Collaborative location and activity recommendations with gps history data. 2010. In: Proceedings of WWW' 10.
-
- Quercia D, Lathia N, Calabrese F, Lorenzo GD, Crowcroft J. Recommending social events from mobile phone location data. 2010. In: Proceedings of IEEE ICDM '10.
-
- Scellato S, Mascolo C, Musolesi M, Crowcroft J. Track globally, deliver locally: Improving content delivery networks by tracking geographic social cascades. 2011. In: Proceedings of WWW' 11.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

