Valley-selective circular dichroism of monolayer molybdenum disulphide

Abstract

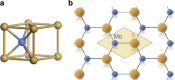
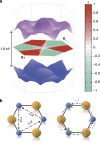
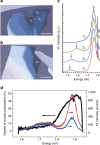
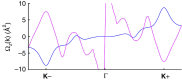
A two-dimensional honeycomb lattice harbours a pair of inequivalent valleys in the k-space electronic structure, in the vicinities of the vertices of a hexagonal Brillouin zone, K(±). It is particularly appealing to exploit this emergent degree of freedom of charge carriers, in what is termed 'valleytronics'. The physics of valleys mimics that of spin, and will make possible devices, analogous to spintronics, such as valley filter and valve, and optoelectronic Hall devices, all very promising for next-generation electronics. The key challenge lies with achieving valley polarization, of which a convincing demonstration in a two-dimensional honeycomb structure remains evasive. Here we show, using first principles calculations, that monolayer molybdenum disulphide is an ideal material for valleytronics, for which valley polarization is achievable via valley-selective circular dichroism arising from its unique symmetry. We also provide experimental evidence by measuring the circularly polarized photoluminescence on monolayer molybdenum disulphide, which shows up to 50% polarization.

Figure 1. The crystal structure of monolayer MoS₂.

(a) Coordination environment of Mo (blue sphere) in the structure. Sulphur is shown as golden spheres. (b) A top view of the monolayer MoS₂ lattice, emphasizing the connection to a honeycomb lattice. In our calculations, we used an optimized structure at the level of local density approximation in density functional theory. The shaded region bounded by dashed lines corresponds to one primitive cell. The unit cell parameter is a=3.12 Å, and the vertical separation between sulphur layers is 3.11 Å.

Figure 2. Valley-selective CD of monolayer MoS₂.

(a) Top valence band (blue) and bottom conduction band (pink). The centre hexagon is the Brillouin zone colour-coded by the degree of circular polarization, η(k), as defined in the text. The vector connecting K₊ and K₋ is perpendicular to Mo-S bond in the crystal structure in Fig. 1b. (b) Schematic of phase winding on the MoS₂ lattice that gives rise to the chiral optical selectivity. Left panel: the contribution to phase winding from the Bloch lattice phase, where τ=±1 is the valley index, and s=1,2 corresponding to the S and Mo sites (isospin index). Right panel: the phase winding under a threefold rotation. The green axes indicate the rotation of local atomic coordinates that leads to the azimuth dissynchronization.

Figure 3. Experimental measurements of circularly polarized PL of monolayer MoS2.

(a) and (b) Optical images of one-to-four-layer samples (1L to 4L) on which micro-PL is performed, where 1L, 2L, 3L and 4L regions are labelled. The scale bars correspond to 5 microns. (c) Micro-PL of monolayer and few-layer MoS₂ at 300 K. Each spectrum is normalized by its maximum intensity. Arrows indicate the lowest-energy peak of each spectrum. (d) Circularly polarized micro-PL of monolayer MoS₂ at 83 K, along with the degree of circular polarization of the PL spectra. The red and blue curves correspond to the intensities of σ⁺ and σ⁻ polarizations, respectively, in the luminescence spectrum. The black curve is the net degree of polarization.

Figure 4. Berry curvature, Ω_n,z(k), of bands across the bandgap.

The blue curve corresponds to the top of valence bands. The red curve corresponds to the bottom of conduction bands. The Berry curvatures of the states along the K₋−Γ−K₊ path of the Brillouin zone are plotted. The value of Berry curvature is large for the conduction band at the zone centre, where bands are degenerate.