Bistability, bifurcations, and Waddington's epigenetic landscape

Abstract

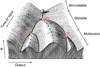
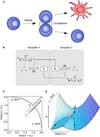
Waddington's epigenetic landscape is probably the most famous and most powerful metaphor in developmental biology. Cells, represented by balls, roll downhill through a landscape of bifurcating valleys. Each new valley represents a possible cell fate and the ridges between the valleys maintain the cell fate once it has been chosen. Here I examine models of two important developmental processes - cell-fate induction and lateral inhibition - and ask whether the landscapes for these models at least qualitatively resemble Waddington's picture. For cell-fate induction, the answer is no. The commitment of a cell to a new fate corresponds to the disappearance of a valley from the landscape, not the splitting of one valley into two, and it occurs through a type of bifurcation - a saddle-node bifurcation - that possesses an intrinsic irreversibility that is missing from Waddington's picture. Lateral inhibition, a symmetrical cell-cell competition process, corresponds better to Waddington's picture, with one valley reversibly splitting into two through a pitchfork bifurcation. I propose an alternative epigenetic landscape that has numerous valleys and ridges right from the start, with the process of cell-fate commitment corresponding to the irreversible disappearance of some of these valleys and ridges, via cell-fate induction, complemented by the creation of new valleys and ridges through processes like cell-cell competition.

Figure 1

Waddington’s epigenetic landscape. Adapted from [1]. Differentiating cells are represented by a ball rolling through a changing potential surface. At the outset of development, the ball can also represent a region of cytoplasm in a fertilized egg. New valleys represent alternative cell fates, and ridges keep cells from switching fates. At the back of the landscape, the potential surface is monostable—there is a single valley. When the valley splits the landscape becomes bistable and then multistable. The solid black lines represent stable steady states, the dashed lines represent unstable steady states, and the red circles represent pitchfork bifurcations (Ψ).

Figure 2. Cell fate induction

(A) Schematic view of a cell fate induction process. (B) A simple mathematical model of a positive feedback system that could trigger and maintain differentiation. (C) Rate-balance analysis, showing the stable steady states (SSS) and unstable steady state (USS). (D) The potential function. The stable steady states lie at the bottoms of valleys and the unstable steady state sits at the top of a ridge. The values assumed for the parameters in Eq 3 are α₀ = 0, α₁ = 4, β=1.1, and K = 2. (E) A saddle-node epigenetic landscape. The input (α₀) increases from 0 to 1.8 as time increases, and the potential is calculated according to Eq 4. Solid lines denote stable steady states (valley bottoms), and the dashed line represents the unstable steady state (the top of the ridge between the two valleys). Cell fate commitment occurs when the left-hand valley and the ridge meet each other and disappear at a saddle-node bifurcation (SN).

Figure 3. Lateral inhibition: competition between two daughter cells for expression of a signaling molecule

(A) Schematic view, with the blue cells possessing high levels of Delta and the red cell possessing a low level of Delta. (B) Mathematical depiction of the mutual inhibition of the synthesis of a Delta-like protein x by x in a neighboring cell. (C) Steady-states in the lateral inhibition model. The parameters chosen for the model (Eqs 6 and 7) are α = 2, β = 1, and n = 4. The interaction strength I is taken as the input to the system, and is varied from 0 to 1. At I = 0.5, the system goes through a pitchfork bifurcation (denoted Ψ). (D) The potential landscape of a lateral inhibition process. At the pitchfork bifurcation, one cell goes one way and the other one goes the other.