Fast alignment of fragmentation trees

Abstract

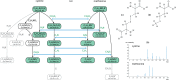
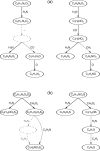
Motivation: Mass spectrometry allows sensitive, automated and high-throughput analysis of small molecules such as metabolites. One major bottleneck in metabolomics is the identification of 'unknown' small molecules not in any database. Recently, fragmentation tree alignments have been introduced for the automated comparison of the fragmentation patterns of small molecules. Fragmentation pattern similarities are strongly correlated with the chemical similarity of the molecules, and allow us to cluster compounds based solely on their fragmentation patterns.

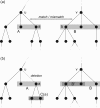
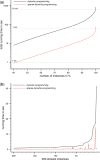
Results: Aligning fragmentation trees is computationally hard. Nevertheless, we present three exact algorithms for the problem: a dynamic programming (DP) algorithm, a sparse variant of the DP, and an Integer Linear Program (ILP). Evaluation of our methods on three different datasets showed that thousands of alignments can be computed in a matter of minutes using DP, even for 'challenging' instances. Running times of the sparse DP were an order of magnitude better than for the classical DP. The ILP was clearly outperformed by both DP approaches. We also found that for both DP algorithms, computing the 1% slowest alignments required as much time as computing the 99% fastest.

Fig. 1.

Optimal fragmentation tree alignment for cystine (11 losses) and methionine (6 losses) from the Orbitrap dataset (a). (b) Fragmentation mass spectra of cystine and methionine. The mass spectra do not share peaks. Molecular structures of cystine (c) and methionine (d). The molecular structures are not known to the alignment method. The alignment detects the common fragmentation path of formic acid–ammonia–ethylene losses and the separate ammonia branch. Additionally, it finds the methylthiol loss, which occurs at a later stage in cystine

Fig. 2.

Two alignments of fragmentation trees based on edge similarities. Nodes represent molecular formulas of the fragments, edges represent molecular formulas of the losses. (a) A gap (−) is introduced for the missing CO loss in the left tree (dashed edge and node). Losses CO and CH₃ are aligned by a mismatch (dotted edges). (b) In the left tree, the fragment after loosing H₃N is missing (dashed edges and node), whereas the fragment after further loss of C₂H₂ is observed. To account for missing fragments, we introduce the join operation. It allows to align the two successive losses H₃N and C₂H₂ in the right tree to a single loss C₂H₅N in the left tree (dotted edges). Fragments may be missing because the corresponding peak was not detected, for example

Fig. 3.

Representation of the match and the deleteL recurrences of the DP algorithm. (a) match_u,v[A, B] is the best score of matching edge ua on edge vb, such that maximally the children A of u and B of v are used. (b) deleteL_u,v[A, B] is the best score for deleting edge ua, such that maximally the children A of u and B of v are used. A subset B′⊆B of the children of v can now be matched to the children of a

Fig. 4.

Running times for the Hill dataset with 5151 individual alignments. (a) Total running times when instances are sorted by individual running times. For any fraction x%, we calculate the total running time of the x%, instances for which the alignment was computed faster than for any of the remaining instances. For example at 50% one can find the running time that was needed to compute the 50% fastest instances. For each algorithm, instances were sorted separately. Note the logarithmic y-axis. (b) Individual running times for the 200 slowest instances of the classical DP algorithm. Instances are sorted by their running time for the classical DP algorithm. One can see that running times of the classical DP are outperformed by that of the sparse DP