Efficient simulation and likelihood methods for non-neutral multi-allele models
- PMID: 22697240
- PMCID: PMC3375650
- DOI: 10.1089/cmb.2012.0033
Efficient simulation and likelihood methods for non-neutral multi-allele models
Abstract
Throughout the 1980s, Simon Tavaré made numerous significant contributions to population genetics theory. As genetic data, in particular DNA sequence, became more readily available, a need to connect population-genetic models to data became the central issue. The seminal work of Griffiths and Tavaré (1994a , 1994b , 1994c) was among the first to develop a likelihood method to estimate the population-genetic parameters using full DNA sequences. Now, we are in the genomics era where methods need to scale-up to handle massive data sets, and Tavaré has led the way to new approaches. However, performing statistical inference under non-neutral models has proved elusive. In tribute to Simon Tavaré, we present an article in spirit of his work that provides a computationally tractable method for simulating and analyzing data under a class of non-neutral population-genetic models. Computational methods for approximating likelihood functions and generating samples under a class of allele-frequency based non-neutral parent-independent mutation models were proposed by Donnelly, Nordborg, and Joyce (DNJ) (Donnelly et al., 2001). DNJ (2001) simulated samples of allele frequencies from non-neutral models using neutral models as auxiliary distribution in a rejection algorithm. However, patterns of allele frequencies produced by neutral models are dissimilar to patterns of allele frequencies produced by non-neutral models, making the rejection method inefficient. For example, in some cases the methods in DNJ (2001) require 10(9) rejections before a sample from the non-neutral model is accepted. Our method simulates samples directly from the distribution of non-neutral models, making simulation methods a practical tool to study the behavior of the likelihood and to perform inference on the strength of selection.
Figures
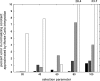
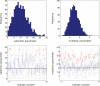
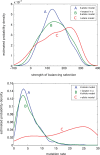
References
-
- Buzbas E.O. Joyce P. Maximum likelihood estimates under k-allele models with selection can be numerically unstable. Ann. Appl. Stat. 2009;3:1147–1162.
-
- Davis P.J. Rabinowitz P. Methods of Numerical Integration. Academic Press; New York: 1984.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials

