Being critical of criticality in the brain
- PMID: 22701101
- PMCID: PMC3369250
- DOI: 10.3389/fphys.2012.00163
Being critical of criticality in the brain
Abstract
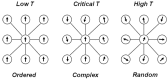
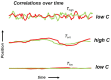
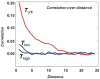
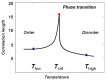
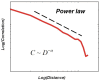
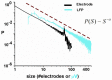
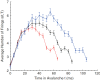
Relatively recent work has reported that networks of neurons can produce avalanches of activity whose sizes follow a power law distribution. This suggests that these networks may be operating near a critical point, poised between a phase where activity rapidly dies out and a phase where activity is amplified over time. The hypothesis that the electrical activity of neural networks in the brain is critical is potentially important, as many simulations suggest that information processing functions would be optimized at the critical point. This hypothesis, however, is still controversial. Here we will explain the concept of criticality and review the substantial objections to the criticality hypothesis raised by skeptics. Points and counter points are presented in dialog form.
Keywords: Ising model; avalanche; criticality; multi-electrode array; network; scale-free; statistical physics.
Figures
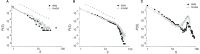
References
-
- Bak P. (1996). How Nature Works: The Science of Self-Organized Criticality. New York, NY: Copernicus
LinkOut - more resources
Full Text Sources

