Investigating hospital heterogeneity with a multi-state frailty model: application to nosocomial pneumonia disease in intensive care units

Abstract

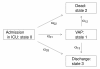
Background: Multistate models have become increasingly useful to study the evolution of a patient's state over time in intensive care units ICU (e.g. admission, infections, alive discharge or death in ICU). In addition, in critically-ill patients, data come from different ICUs, and because observations are clustered into groups (or units), the observed outcomes cannot be considered as independent. Thus a flexible multi-state model with random effects is needed to obtain valid outcome estimates.

Methods: We show how a simple multi-state frailty model can be used to study semi-competing risks while fully taking into account the clustering (in ICU) of the data and the longitudinal aspects of the data, including left truncation and right censoring. We suggest the use of independent frailty models or joint frailty models for the analysis of transition intensities. Two distinct models which differ in the definition of time t in the transition functions have been studied: semi-Markov models where the transitions depend on the waiting times and nonhomogenous Markov models where the transitions depend on the time since inclusion in the study. The parameters in the proposed multi-state model may conveniently be computed using a semi-parametric or parametric approach with an existing R package FrailtyPack for frailty models. The likelihood cross-validation criterion is proposed to guide the choice of a better fitting model.

Results: We illustrate the use of our approach though the analysis of nosocomial infections (ventilator-associated pneumonia infections: VAP) in ICU, with "alive discharge" and "death" in ICU as other endpoints. We show that the analysis of dependent survival data using a multi-state model without frailty terms may underestimate the variance of regression coefficients specific to each group, leading to incorrect inferences. Some factors are wrongly significantly associated based on the model without frailty terms. This result is confirmed by a short simulation study. We also present individual predictions of VAP underlining the usefulness of dynamic prognostic tools that can take into account the clustering of observations.

Conclusions: The use of multistate frailty models allows the analysis of very complex data. Such models could help improve the estimation of the impact of proposed prognostic features on each transition in a multi-centre study. We suggest a method and software that give accurate estimates and enables inference for any parameter or predictive quantity of interest.

Figure 1

The “disability Model”.

Figure 2

Random centre-specific effect as estimated by posterior distribution for the different transitions. The clusters have been ordered (ascending order) by the number of subjects in the cluster.

Figure 3

Predicted probabilities (see formula (7)) of a patient in state 0 developing VAP betweent∗andt∗ + 3days for a patient from the 16 different centers. Predictions given for a men, aged > 62, SAPSII<33, with medicine admission, no chronic diseases, no diabetes, no ARDS, no Trauma, with shock, no acute respiratory failure, no antimicrobials, with inotropes, with enteral and parenteral nutrition.