Surface phonons, elastic response, and conformal invariance in twisted kagome lattices
- PMID: 22733727
- PMCID: PMC3412002
- DOI: 10.1073/pnas.1119941109
Surface phonons, elastic response, and conformal invariance in twisted kagome lattices
Abstract
Model lattices consisting of balls connected by central-force springs provide much of our understanding of mechanical response and phonon structure of real materials. Their stability depends critically on their coordination number z. d-dimensional lattices with z = 2d are at the threshold of mechanical stability and are isostatic. Lattices with z < 2d exhibit zero-frequency "floppy" modes that provide avenues for lattice collapse. The physics of systems as diverse as architectural structures, network glasses, randomly packed spheres, and biopolymer networks is strongly influenced by a nearby isostatic lattice. We explore elasticity and phonons of a special class of two-dimensional isostatic lattices constructed by distorting the kagome lattice. We show that the phonon structure of these lattices, characterized by vanishing bulk moduli and thus negative Poisson ratios (equivalently, auxetic elasticity), depends sensitively on boundary conditions and on the nature of the kagome distortions. We construct lattices that under free boundary conditions exhibit surface floppy modes only or a combination of both surface and bulk floppy modes; and we show that bulk floppy modes present under free boundary conditions are also present under periodic boundary conditions but that surface modes are not. In the long-wavelength limit, the elastic theory of all these lattices is a conformally invariant field theory with holographic properties (characteristics of the bulk are encoded on the sample boundary), and the surface waves are Rayleigh waves. We discuss our results in relation to recent work on jammed systems. Our results highlight the importance of network architecture in determining floppy-mode structure.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
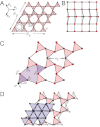
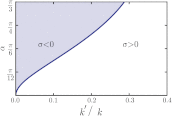
 on a plateau beginning at
on a plateau beginning at  defining a length scale l∗ = 1/q∗. (B) Phonon spectrum for α > 0 and k′ = 0. The plateau along ΓM defines
defining a length scale l∗ = 1/q∗. (B) Phonon spectrum for α > 0 and k′ = 0. The plateau along ΓM defines  and its onset at qα ∼ ωα defines a length lα ∼ 1/| sin α|.
and its onset at qα ∼ ωα defines a length lα ∼ 1/| sin α|.

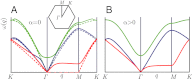
 as a function of qxaL for lattice Rayleigh surface waves for α = π/20, π/10, 3π/20, π/5, π/4, in order from bottom to top. Smooth curves are the analytic results from a transfer matrix calculation, and dots are from direct numerical calculations. The dashed line is the continuum Rayleigh limit
as a function of qxaL for lattice Rayleigh surface waves for α = π/20, π/10, 3π/20, π/5, π/4, in order from bottom to top. Smooth curves are the analytic results from a transfer matrix calculation, and dots are from direct numerical calculations. The dashed line is the continuum Rayleigh limit  . Curves at smaller α break away from this curve at smaller values of qy than do those at large α. At α = π/4,
. Curves at smaller α break away from this curve at smaller values of qy than do those at large α. At α = π/4,  diverges at qyaL = π. The inset plots
diverges at qyaL = π. The inset plots  as a function of qxlα for different α. The lower curve in the inset (black) is the α-independent scaling function of qylα reached in the α → 0 limit. The other curves from top to bottom are for α = π/25, π/12, π/9, and π/6 (chosen to best present results rather than to match the curves in the main figure). Curves for α < π/15 are essentially indistinguishable from the scaling limit. The curve at α = π/6 stops because qy < π/aL.
as a function of qxlα for different α. The lower curve in the inset (black) is the α-independent scaling function of qylα reached in the α → 0 limit. The other curves from top to bottom are for α = π/25, π/12, π/9, and π/6 (chosen to best present results rather than to match the curves in the main figure). Curves for α < π/15 are essentially indistinguishable from the scaling limit. The curve at α = π/6 stops because qy < π/aL.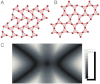
Comment in
-
Topological soft matter: Kagome lattices with a twist.Proc Natl Acad Sci U S A. 2012 Jul 31;109(31):12266-7. doi: 10.1073/pnas.1209950109. Epub 2012 Jul 23. Proc Natl Acad Sci U S A. 2012. PMID: 22826235 Free PMC article. No abstract available.
References
-
- Maxwell JC. On the calculation of the equilibrium and stiffness of frames. Philos Mag. 1865;27:294.
-
- Calladine CR. Buckminster fuller “tensegrity” structures and Clerk Maxwell rules for the construction of stiff frames. Int J Solids Struct. 1978;14:161–172.
-
- Asimow L, Roth B. Rigidity of graphs. Trans Am Math Soc. 1978;245:279–289.
-
- Asimow L, Roth B. Rigidity of graphs 2. J Math Anal Appl. 1979;68:171–190.
-
- Connelly R. Rigidity and energy. Invent Math. 1982;66:11–33.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

