Modelling cell polarization driven by synthetic spatially graded Rac activation
- PMID: 22737059
- PMCID: PMC3380869
- DOI: 10.1371/journal.pcbi.1002366
Modelling cell polarization driven by synthetic spatially graded Rac activation
Abstract
The small GTPase Rac is known to be an important regulator of cell polarization, cytoskeletal reorganization, and motility of mammalian cells. In recent microfluidic experiments, HeLa cells endowed with appropriate constructs were subjected to gradients of the small molecule rapamycin leading to synthetic membrane recruitment of a Rac activator and direct graded activation of membrane-associated Rac. Rac activation could thus be triggered independent of upstream signaling mechanisms otherwise responsible for transducing activating gradient signals. The response of the cells to such stimulation depended on exceeding a threshold of activated Rac. Here we develop a minimal reaction-diffusion model for the GTPase network alone and for GTPase-phosphoinositide crosstalk that is consistent with experimental observations for the polarization of the cells. The modeling suggests that mutual inhibition is a more likely mode of cell polarization than positive feedback of Rac onto its own activation. We use a new analytical tool, Local Perturbation Analysis, to approximate the partial differential equations by ordinary differential equations for local and global variables. This method helps to analyze the parameter space and behaviour of the proposed models. The models and experiments suggest that (1) spatially uniform stimulation serves to sensitize a cell to applied gradients. (2) Feedback between phosphoinositides and Rho GTPases sensitizes a cell. (3) Cell lengthening/flattening accompanying polarization can increase the sensitivity of a cell and stabilize an otherwise unstable polarization.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
 represents the strength of PI feedback to Rac. Arrows represent upregulation and bars represent inhibition. In all cases, proposed interactions between GTPases and PIs are taken from the literature , –.
represents the strength of PI feedback to Rac. Arrows represent upregulation and bars represent inhibition. In all cases, proposed interactions between GTPases and PIs are taken from the literature , –.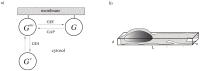
 . The width is constrained by the microfluidic channels in experiments .
. The width is constrained by the microfluidic channels in experiments .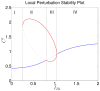
 ) with
) with  , the basal Rac GEF activity level, as bifurcation parameter. Here
, the basal Rac GEF activity level, as bifurcation parameter. Here  (no PI feedback),
(no PI feedback),  and all other parameters as in Table 1. The monotone increasing (blue) curve represents the HSS of the original system and is stable to homogeneous perturbations. Elliptical (red) arcs represent additional equilibria found in the LPA-system. Stability to small heterogeneous perturbations is indicated by solid lines vs instability shown by dotted lines. Region I is insensitive to perturbations, II is polarizable with sufficiently large perturbations, III is hypersensitive (Turing unstable), IV is insensitive but overstimulated. Similar results are seen when plotting
and all other parameters as in Table 1. The monotone increasing (blue) curve represents the HSS of the original system and is stable to homogeneous perturbations. Elliptical (red) arcs represent additional equilibria found in the LPA-system. Stability to small heterogeneous perturbations is indicated by solid lines vs instability shown by dotted lines. Region I is insensitive to perturbations, II is polarizable with sufficiently large perturbations, III is hypersensitive (Turing unstable), IV is insensitive but overstimulated. Similar results are seen when plotting  or
or  on the vertical axis.
on the vertical axis.
 (Region II in Figure 3). Patterning is induced by a large local perturbation applied to active Rac at
(Region II in Figure 3). Patterning is induced by a large local perturbation applied to active Rac at  . Identical behaviour is seen when this perturbation is applied to active Cdc42. Right panel:
. Identical behaviour is seen when this perturbation is applied to active Cdc42. Right panel:  (Region III in Figure 3). Patterning is induced by random noise of size
(Region III in Figure 3). Patterning is induced by random noise of size  in the initial conditions. Similar (complementary) kymographs of Rac (Rho) are obtained (not shown).
in the initial conditions. Similar (complementary) kymographs of Rac (Rho) are obtained (not shown).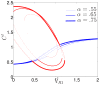
 values. For larger
values. For larger  values, the model is more sensitive to heterogeneous stimuli.
values, the model is more sensitive to heterogeneous stimuli.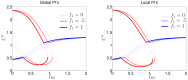
 and multiple values of
and multiple values of  . Left panel: PI variables treated as fast (global) LPA variables. Right panel: PI variables treated as slow (local) LPA variables. Note the simple linear leftwards shift as
. Left panel: PI variables treated as fast (global) LPA variables. Right panel: PI variables treated as slow (local) LPA variables. Note the simple linear leftwards shift as  increases in both panels.
increases in both panels.
 , and other parameters as in Table 1. The grey region is bistable and the white is Turing unstable. The linearity of this bifurcation curve is both qualitatively and quantitatively consistent with the linear shift of the bifurcation diagrams seen in Figure 6.
, and other parameters as in Table 1. The grey region is bistable and the white is Turing unstable. The linearity of this bifurcation curve is both qualitatively and quantitatively consistent with the linear shift of the bifurcation diagrams seen in Figure 6.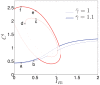
 is increased, the stable Region I of Figure 3 at low
is increased, the stable Region I of Figure 3 at low  values vanishes, eliminating the hysteresis associated with the stable to bistable transition.
values vanishes, eliminating the hysteresis associated with the stable to bistable transition.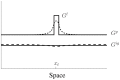
 represents the slow diffusing active form which has a local component
represents the slow diffusing active form which has a local component  near the applied pertubation at
near the applied pertubation at  and a global behaviour
and a global behaviour  away from it. Since diffusion is slow, they do not directly influence each other on a short time scale.
away from it. Since diffusion is slow, they do not directly influence each other on a short time scale.  is fast diffusing and takes on only a global behaviour away
is fast diffusing and takes on only a global behaviour away  . Solid curves qualitativly represent this pulse in the idealized diffusion limit and dashed curves represent the same situation with finite rates of diffusion.
. Solid curves qualitativly represent this pulse in the idealized diffusion limit and dashed curves represent the same situation with finite rates of diffusion.References
-
- Song L, Nadkarni SM, Bodeker HU, Beta C, Bae A, et al. Dictyostelium discoideum chemo- taxis: Threshold for directed motion. Eur J Cell Biol. 2006;85:981– 989. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

