On measures of association among genetic variables

Abstract

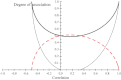
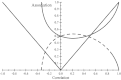
Systems involving many variables are important in population and quantitative genetics, for example, in multi-trait prediction of breeding values and in exploration of multi-locus associations. We studied departures of the joint distribution of sets of genetic variables from independence. New measures of association based on notions of statistical distance between distributions are presented. These are more general than correlations, which are pairwise measures, and lack a clear interpretation beyond the bivariate normal distribution. Our measures are based on logarithmic (Kullback-Leibler) and on relative 'distances' between distributions. Indexes of association are developed and illustrated for quantitative genetics settings in which the joint distribution of the variables is either multivariate normal or multivariate-t, and we show how the indexes can be used to study linkage disequilibrium in a two-locus system with multiple alleles and present applications to systems of correlated beta distributions. Two multivariate beta and multivariate beta-binomial processes are examined, and new distributions are introduced: the GMS-Sarmanov multivariate beta and its beta-binomial counterpart.

Figure 1

Measures of association of two bivariate Gaussian variables as a function of their correlation (ρ). The straight lines give the strength of the association as measured by the absolute value of ρ. The dotted (‘holds water’: θ) and dashed (‘spills water’: 1 − θ) lines depict the relative contributions to the Kullback-Leibler distance due to discrepancies under independence and dependence models, respectively. Values of the association measure γ=2θ − 1 are represented by the dark solid line.

Figure 2

Indexes of association as a function of the coefficient of correlation in an equi-correlated trivariate normal distribution. The thick solid line gives the relative Kullback-Leibler discrepancy between distributions when independence holds (θ), and the dashed line gives the relative discrepancy when association is true (1 − θ). The thin line gives the trajectory of γ=2θ − 1.

Figure 3

Discrepancies from independence to association (θ, solid line), and from association to independence (1 − θ, dashed line) as a fraction of the Kullback-Leibler distance between two tetravariate normal distributions. The straight lines give the absolute values of the correlation ρ.

Figure 4

Scatter diagrams of 5000 samples from each of four Olkin-Liu bivariate beta distributions. Plot 1 illustrates a strong association with essentially no correlation. Plot 2 (‘meteorite’) depicts a limitation of the correlation as a parameter for describing association. Plot 3 suggests association clearly. Plot 4 shows a bivariate distribution that is not trivial: the true correlation (0.46) arises primarily due to weaker association in the ‘middle’ of the bivariate sampling space.

Figure 5

Plots of the densities of four Lee-Sarmanov bivariate beta distributions having the same Beta (2,2) marginal distributions but differing in the strength of association: as the correlation increases multi-modality emerges.