On the origin of the unusual behavior in the stretching of single-stranded DNA

Abstract

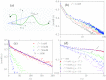
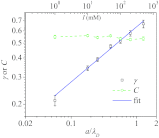
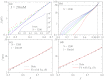
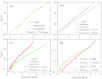
Force-extension curves (FECs), which quantify the response of a variety of biomolecules subject to mechanical force (f), are often quantitatively fit using worm-like chain (WLC) or freely jointed chain (FJC) models. These models predict that the chain extension, x, normalized by the contour length increases linearly at small f and at high forces scale as x ~ (1 - f(-α)), where α = 0.5 for WLC and unity for FJC. In contrast, experiments on single-stranded DNA (ssDNA) show that over a range of f and ionic concentration, x scales as x ~ ln f, which cannot be explained using WLC or FJC models. Using theory and simulations we show that this unusual behavior in FEC in ssDNA is due to sequence-independent polyelectrolyte effects. We show that the x ~ ln f arises because in the absence of force the tangent correlation function, quantifying chain persistence, decays algebraically on length scales on the order of the Debye length. Our theory, which is most appropriate for monovalent salts, quantitatively fits the experimental data and further predicts that such a regime is not discernible in double-stranded DNA.

Figure 1

(a) A cartoon of the polymer chain showing tangent vectors at s_i and s_j along the chain. The angle θ(s = |s_j − s_i|) between the two vectors is shown. The average value over all possible conformation of the chain ⟨cos θ(s)⟩ is the tangent correlation along the chain. The length scale over which ⟨cos θ(s)⟩ decays at f = 0 is the measure of the chain persistence length. (b) At I = 1 mM, all the curves with various N values (from bottom to top N = 100, 200, 800, 1600) show that there are strong finite size effects. Only when N exceeds 1600 do the curves converge. (c) ⟨cos θ(s)⟩ in log-linear scale for N = 1600 and at various I. The solid line is a double exponential fit using ⟨cos θ⟩ = (1 − β) exp (− s/λ₁) + β exp (− s/λ₂), with β ≈ 0.358 and λ₁ ≈ 1.02a and λ₂ ≈ 179.11a. (d) To identify the power law behavior the data in (c) are shown as a log-log plot. The curves at various ionic strength clearly show that ⟨cos θ(s)⟩ decays as a power law on scale s ⩽ λ_D. The arrows correspond to λ_D. The solid line is the double exponential fit.

Figure 2

The values of C and γ extracted from the simulation data of ⟨cos θ(s)⟩ for PE chains with N = 1600 using Eq. 4.

Figure 3

(a) Force-extension curves (FECs) for various N values at I = 20 mM. The N values from top to bottom are 100, 200, 400, 1600, and 3200 (solid line). The inset shows the FEC for N = 3200. (b) FECs for a PE chain with N = 3200 at various values of I. The values of I from bottom to top are 1, 10, 20, 50, 100, 200, and 3000 mM. The dashed line is plotted using $x\approx 1-{\xi }_t/\sqrt{{\lambda }_K^2+a^2}$ Eq. 10. (c) and (d) Fits using Eq. 8 to simulation data for a chain with N = 3200 at I = 20 and 50 mM, respectively. See text for the values of the parameters.

Figure 4

Single-parameter (using the contour length L_c as the fit parameter) fits of simulated FECs to experimental data of ssDNA in Na⁺ solutions. The high quality of the fits for I = 1 mM (a), 10 mM (b), 100 mM (c), 500 mM and 1000 mM (d) indicates that electrostatic interactions play a dominant role in the stretching of ssDNA.