Subject-specific functional localizers increase sensitivity and functional resolution of multi-subject analyses
- PMID: 22784644
- PMCID: PMC3477490
- DOI: 10.1016/j.neuroimage.2012.06.065
Subject-specific functional localizers increase sensitivity and functional resolution of multi-subject analyses
Abstract
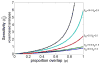
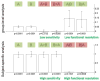
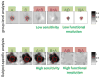
One important goal of cognitive neuroscience is to discover and explain properties common to all human brains. The traditional solution for comparing functional activations across brains in fMRI is to align each individual brain to a template brain in a Cartesian coordinate system (e.g., the Montreal Neurological Institute template). However, inter-individual anatomical variability leads to decreases in sensitivity (ability to detect a significant activation when it is present) and functional resolution (ability to discriminate spatially adjacent but functionally different neural responses) in group analyses. Subject-specific functional localizers have been previously argued to increase the sensitivity and functional resolution of fMRI analyses in the presence of inter-subject variability in the locations of functional activations (e.g., Brett et al., 2002; Fedorenko and Kanwisher, 2009, 2011; Fedorenko et al., 2010; Kanwisher et al., 1997; Saxe et al., 2006). In the current paper we quantify this dependence of sensitivity and functional resolution on functional variability across subjects in order to illustrate the highly detrimental effects of this variability on traditional group analyses. We show that analyses that use subject-specific functional localizers usually outperform traditional group-based methods in both sensitivity and functional resolution, even when the same total amount of data is used for each analysis. We further discuss how the subject-specific functional localization approach, which has traditionally only been considered in the context of ROI-based analyses, can be extended to whole-brain voxel-based analyses. We conclude that subject-specific functional localizers are particularly well suited for investigating questions of functional specialization in the brain. An SPM toolbox that can perform all of the analyses described in this paper is publicly available, and the analyses can be applied retroactively to any dataset, provided that multiple runs were acquired per subject, even if no explicit "localizer" task was included.
Copyright © 2012 Elsevier Inc. All rights reserved.
Figures



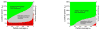



References
-
- Aguirre GK, Detre JA. The development and future of perfusion fMRI for dynamic imaging of human brain activity. NeuroImage (in press) - PubMed
-
- Amunts K, Schleicher A, Bürgel U, Mohlberg H, Uylings HB, Zilles K. Broca’s region revisited: Cytoarchitecture and intersubject variability. J Comp Neurol. 1999;412(2):319–41. - PubMed
-
- Barbier EL, Marrett S, Danek A, Vortmeyer A, van Gelderen P, Duyn J, Bandettini P, Grafman J, Koretsky AP. Imaging cortical anatomy by high-resolution MR at 3.0T: Detection of the stripe of Gennari in visual area 17. Magn Reson Med. 2002;48:735–738. - PubMed
-
- Brett M, Johnsrude IS, Owen AM. The problem of functional localization in the human brain. Nature Reviews Neuroscience. 2002;3(3):243–249. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

