The contribution of age structure to cell population responses to targeted therapeutics

Abstract

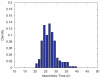
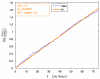
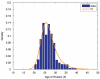
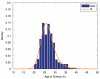
Cells grown in culture act as a model system for analyzing the effects of anticancer compounds, which may affect cell behavior in a cell cycle position-dependent manner. Cell synchronization techniques have been generally employed to minimize the variation in cell cycle position. However, synchronization techniques are cumbersome and imprecise and the agents used to synchronize the cells potentially have other unknown effects on the cells. An alternative approach is to determine the age structure in the population and account for the cell cycle positional effects post hoc. Here we provide a formalism to use quantifiable lifespans from live cell microscopy experiments to parameterize an age-structured model of cell population response.

Fig. 1

Plot of an histogram (H_i)_1≤i≤Na representing the IMT distribution of a population of PC-9 lung cancer cells. The data are from Tyson et al. (in press) and the bin width is $\Delta a=\frac{10}{8}$.

Fig. 2

The evolution of the total population N(t) is plotted on log-scale (blue) (the data are from Tyson et al., in press). The data are well-fitted with a line of slope λ = 0.022 (correlation coefficient: R² = 0.9967). This is evidence that the total population is growing exponentially fast with exponential constant λ. Thus, N(t) = exp^λtN(0), and if t* is the population doubling time, then N(t*) = 2N(0), and t* = ln 2/λ. (For interpretation of the references to color in this figure caption, the reader is referred to the web version of this article.)

Fig. 3

The two different gamma functions and their corresponding division rate β(a) are plotted for coefficients m=17 and σ = 2.

Fig. 4

Left: The division rate β(a) is obtained numerically from (14) by using an EMG with coefficients m=22, σ = 2 and β₀ = 0.2 to fit I_∞ (19). Right: The formula for β, as an error function with these same three parameters, is numerically indistinguishable from the numerically obtained β(R² = 1).

Fig. 5

Fitting of experimental data in Tyson et al. (in press) with the model (21). The fitting parameters are β₀ = 0.14204, m = 24.456 and σ = 3.3451. The correlation coefficient is R² = 0.95363 and the integral of ${\tilde{I}}_{\infty }(a\mid {\beta }_0,m,\sigma )$ is ${\int }_0^{\infty }{\tilde{I}}_{\infty }\left(a\right)da\approx 1.0983$. The formula for the age dependent division rate is β(a) = β₀Erfc((m−a)/σ).

Fig. 6

Fitting of experimental data with the model (26). The fitting parameters are β₀ = 0.17879, m = 25.007, σ = 3.6141 and m = 0.00333. The correlation coefficient is R²=0.95611 and the integral of ${\tilde{I}}_{\infty }(a\mid {\beta }_0,m,\sigma )$ is ${\int }_0^{\infty }{\tilde{I}}_{\infty }\left(a\right)da\approx 1.0132$. The formula for the age dependent division rate is β(a) = β₀Erfc((m−a)/σ).

Fig. 7

Left: Experimental data without erlotinib, with a 50 nM dose and with a 5000 nM dose. The total quantity N(t) is plotted on a log-scale. Right: Numerical simulation of model (1) for f=0, f=0.6 and f=0.84. The curves represent the evolution of ln(P(t)+Q(t)) where $P\left(t\right)≔{\int }_0^{\infty }p(t,a)da$ is the total quantity of proliferating cells at time t. They are obtained by solving Eq. (1) numerically with the parameters of Fig. 6 and with ν = 0.004.