Coding conspecific identity and motion in the electric sense
- PMID: 22807662
- PMCID: PMC3395610
- DOI: 10.1371/journal.pcbi.1002564
Coding conspecific identity and motion in the electric sense
Abstract
Interactions among animals can result in complex sensory signals containing a variety of socially relevant information, including the number, identity, and relative motion of conspecifics. How the spatiotemporal properties of such evolving naturalistic signals are encoded is a key question in sensory neuroscience. Here, we present results from experiments and modeling that address this issue in the context of the electric sense, which combines the spatial aspects of vision and touch, with the temporal aspects of audition. Wave-type electric fish, such as the brown ghost knifefish, Apteronotus leptorhynchus, used in this study, are uniquely identified by the frequency of their electric organ discharge (EOD). Multiple beat frequencies arise from the superposition of the EODs of each fish. We record the natural electrical signals near the skin of a "receiving" fish that are produced by stationary and freely swimming conspecifics. Using spectral analysis, we find that the primary beats, and the secondary beats between them ("beats of beats"), can be greatly influenced by fish swimming; the resulting motion produces low-frequency envelopes that broaden all the beat peaks and reshape the "noise floor". We assess the consequences of this motion on sensory coding using a model electroreceptor. We show that the primary and secondary beats are encoded in the afferent spike train, but that motion acts to degrade this encoding. We also simulate the response of a realistic population of receptors, and find that it can encode the motion envelope well, primarily due to the receptors with lower firing rates. We discuss the implications of our results for the identification of conspecifics through specific beat frequencies and its possible hindrance by active swimming.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

 in Equation (1) with
in Equation (1) with  = 2 (dotted line). The Ornstein-Uhlenbeck process (OUP)
= 2 (dotted line). The Ornstein-Uhlenbeck process (OUP)  is generated using
is generated using  (black dotted curve). (B) Mean contrasts
(black dotted curve). (B) Mean contrasts  standard deviations (STD) of the raw data from the same 8 pairs using the same color scheme as in (A); numerical results calculated directly from Equation (1) (black lines) and approximate theoretical results (circles, see Materials and Methods) showing how the mean contrast (solid black line and solid circles) of the simulation signal
standard deviations (STD) of the raw data from the same 8 pairs using the same color scheme as in (A); numerical results calculated directly from Equation (1) (black lines) and approximate theoretical results (circles, see Materials and Methods) showing how the mean contrast (solid black line and solid circles) of the simulation signal  and the mean
and the mean  STD contrast with
STD contrast with  = 0.6 (dashed black lines and open circles) increase with
= 0.6 (dashed black lines and open circles) increase with  ; Inset: STD/mean contrast for eight pairs of fish. Note that timeplots in Figure 2C, 2D and 2E, the green curve in Figure 3A and the green data point in Figure 3B are from the same recording of a pair of fish, and it will be used as representative data in the later analysis and figures in the case of two fish. (C) Based on the parameter values provided by this representative data, an example of the artificial signal
; Inset: STD/mean contrast for eight pairs of fish. Note that timeplots in Figure 2C, 2D and 2E, the green curve in Figure 3A and the green data point in Figure 3B are from the same recording of a pair of fish, and it will be used as representative data in the later analysis and figures in the case of two fish. (C) Based on the parameter values provided by this representative data, an example of the artificial signal  (see Equation (1); black, only the upper part shown here) is shown and its envelopes E1 (red) and E2 (blue) over 1.2 seconds. Its parameter values are
(see Equation (1); black, only the upper part shown here) is shown and its envelopes E1 (red) and E2 (blue) over 1.2 seconds. Its parameter values are  = 827 Hz,
= 827 Hz,  = 763 Hz,
= 763 Hz,  = 0.143,
= 0.143,  = 0.08,
= 0.08,  = 1. (D) A comparison between E2 (blue) and the amplitude of the second sinusoidal wave:
= 1. (D) A comparison between E2 (blue) and the amplitude of the second sinusoidal wave:  (orange) over 10 seconds.
(orange) over 10 seconds.
 0, black solid curves) is scaled so that its total energy is equal to that of the raw data. The same scaling factor (1
0, black solid curves) is scaled so that its total energy is equal to that of the raw data. The same scaling factor (1 8000) is used to simulate the signal corresponding to the “static” mode (
8000) is used to simulate the signal corresponding to the “static” mode ( = 0, black dashed curves). Note that the rising power in the low frequency range (0–20 Hz) related to the motion disappears. In the case of two fish, the EODfs of the receiving fish and its neighbour were
= 0, black dashed curves). Note that the rising power in the low frequency range (0–20 Hz) related to the motion disappears. In the case of two fish, the EODfs of the receiving fish and its neighbour were  = 827 Hz and
= 827 Hz and  = 763 Hz, respectively, causing a beat frequency of 64 Hz. For three fish, the EODfs of the receiving fish and its two neighbours were
= 763 Hz, respectively, causing a beat frequency of 64 Hz. For three fish, the EODfs of the receiving fish and its two neighbours were  = 831 Hz,
= 831 Hz,  = 740 Hz and
= 740 Hz and  = 889 Hz, respectively, with beat frequencies of 91 Hz and 58 Hz. The secondary beat frequency (i.e. the difference between two beat frequencies,
= 889 Hz, respectively, with beat frequencies of 91 Hz and 58 Hz. The secondary beat frequency (i.e. the difference between two beat frequencies,  ) are highlighted by E2. The parameters used for the simulated signal are
) are highlighted by E2. The parameters used for the simulated signal are  = 0.143,
= 0.143,  = 0.08 for the two fish case, and
= 0.08 for the two fish case, and  = 0.03,
= 0.03,  = 0.08,
= 0.08,  = 0.5
= 0.5 for the three fish case;
for the three fish case;  = 1 in both cases.
= 1 in both cases.
 10−9, dashed line) and (C, D) resolution (defined as the ratio of height to width) of the peak of
10−9, dashed line) and (C, D) resolution (defined as the ratio of height to width) of the peak of  at the beat frequency,
at the beat frequency,  , with increasing
, with increasing  and fixed
and fixed  = 0.1 (left column), or increasing
= 0.1 (left column), or increasing  and fixed
and fixed  = 0.2 (right column). Increasing
= 0.2 (right column). Increasing  improves this resolution, whereas the increases in
improves this resolution, whereas the increases in  decreases this resolution. Other parameters here are the same as those in the case of two fish in Figure 3. 50 independent OU process realizations were used to produce theses averaged plots.
decreases this resolution. Other parameters here are the same as those in the case of two fish in Figure 3. 50 independent OU process realizations were used to produce theses averaged plots.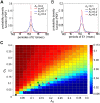
 and
and  changes (A), or when
changes (A), or when  and
and  changes (B). The binwidth is 0.02 msec. A larger
changes (B). The binwidth is 0.02 msec. A larger  produces more periods at precisely
produces more periods at precisely  ; a higher
; a higher  disperses the periods over a broader time interval. (C) The coefficient of variation (CV, the ratio between STD and mean) of the periods of E1 increases with
disperses the periods over a broader time interval. (C) The coefficient of variation (CV, the ratio between STD and mean) of the periods of E1 increases with  , but decreases with
, but decreases with  . Combinations of
. Combinations of  and
and  corresponding to experimental trials are marked by dots with the same color scheme as in Figure 2B.
corresponding to experimental trials are marked by dots with the same color scheme as in Figure 2B.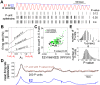
 as input (
as input ( is constant), the firing rate of the P-unit increases with increasing
is constant), the firing rate of the P-unit increases with increasing  . The range of the envelope,
. The range of the envelope,  , is mainly
, is mainly  ] as indicated in equation (6) in Material and Methods. (C) Within a time window of 0.1 second, the number of spikes increases with increasing E2. These data are extracted from recordings (as in Figure 2D) and simulations (as in Figure 3D). (D) Mean time-dependent firing rate (black trace) obtained from 200 independent P-units, each with its own internal noise and baseline firing rate set by the parameter
] as indicated in equation (6) in Material and Methods. (C) Within a time window of 0.1 second, the number of spikes increases with increasing E2. These data are extracted from recordings (as in Figure 2D) and simulations (as in Figure 3D). (D) Mean time-dependent firing rate (black trace) obtained from 200 independent P-units, each with its own internal noise and baseline firing rate set by the parameter  (see panel E), exhibits a time-varying curve similar to E2 (blue trace, as in Figure 2D) of the recording that was used as input to all 200 P-units. The colored trace is an example of the time-varying firing rate of a single P-unit with a P-value of 0.23. (E) Varying
(see panel E), exhibits a time-varying curve similar to E2 (blue trace, as in Figure 2D) of the recording that was used as input to all 200 P-units. The colored trace is an example of the time-varying firing rate of a single P-unit with a P-value of 0.23. (E) Varying  in the P-unit model (equation (7) in Material and Methods) according to the density shown on the top generated a good approximation to the experimentally observed heterogeneity in P-values shown on the bottom (the latter being well-fitted to a log-normal density in [29]). It also leads to a good agreement with the experimental observed envelop-coding ability of P-units in (see Figure S1).
in the P-unit model (equation (7) in Material and Methods) according to the density shown on the top generated a good approximation to the experimentally observed heterogeneity in P-values shown on the bottom (the latter being well-fitted to a log-normal density in [29]). It also leads to a good agreement with the experimental observed envelop-coding ability of P-units in (see Figure S1).
 . (B) Cross-spectra
. (B) Cross-spectra  between E1 and the P-unit response, and cross-spectra
between E1 and the P-unit response, and cross-spectra  between E2 and the P-unit response. (C) Coherence
between E2 and the P-unit response. (C) Coherence  between E1 and the P-unit response, and coherence
between E1 and the P-unit response, and coherence  between E2 and the P-unit response; we compare the coherence functions of P-units with different P-values over 0–20 Hz in the inset, showing that P-units with low P-values can better encode motion-related information than those with high P-values. Results are shown for two fish (left column) and three fish (right column) and P-unit model with P-value of 0.26 (green and black curves), P-value of 0.12 (cyan curves) and a population of 200 P-units with variable P-values as shown in Figure 7E (magenta curves). The recordings in Figure 3 were used as input to the P-unit model (green, cyan, magenta traces); the same parameter values in Figure 3 were used for simulation input (black traces).
between E2 and the P-unit response; we compare the coherence functions of P-units with different P-values over 0–20 Hz in the inset, showing that P-units with low P-values can better encode motion-related information than those with high P-values. Results are shown for two fish (left column) and three fish (right column) and P-unit model with P-value of 0.26 (green and black curves), P-value of 0.12 (cyan curves) and a population of 200 P-units with variable P-values as shown in Figure 7E (magenta curves). The recordings in Figure 3 were used as input to the P-unit model (green, cyan, magenta traces); the same parameter values in Figure 3 were used for simulation input (black traces).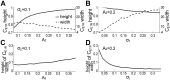
 at the beat frequency,
at the beat frequency,  , and the width (dashed line) of this peak at the coherence value of 0.15 increase and slightly decrease, respectively, with
, and the width (dashed line) of this peak at the coherence value of 0.15 increase and slightly decrease, respectively, with  (with fixed
(with fixed  = 0.1). However (B), the above height and width slightly decrease and strongly increase, respectively, with
= 0.1). However (B), the above height and width slightly decrease and strongly increase, respectively, with  (with fixed
(with fixed  = 0.2). Therefore (C), the height-to-width ratio of this
= 0.2). Therefore (C), the height-to-width ratio of this  peak slightly increases with
peak slightly increases with  , while (D) it decreases rapidly with
, while (D) it decreases rapidly with  . The curves in this figure and next figure are the average results over five artificial signals with
. The curves in this figure and next figure are the average results over five artificial signals with  = [827,737], [827,760], [827,792], [827,704], [740,807]Hz; 50 independent OU processes
= [827,737], [827,760], [827,792], [827,704], [740,807]Hz; 50 independent OU processes  were used to calculate the average for each artificial signal.
were used to calculate the average for each artificial signal.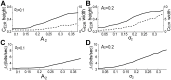
 over the 0–20 Hz range and the width (dashed line, measured at 0.15) increase, with
over the 0–20 Hz range and the width (dashed line, measured at 0.15) increase, with  (and fixed
(and fixed  = 0.1), as well as with
= 0.1), as well as with  (and fixed
(and fixed  = 0.2). Higher mutual information (MI) rate,
= 0.2). Higher mutual information (MI) rate,  , could be obtained over 0–20 Hz with increasing
, could be obtained over 0–20 Hz with increasing  (C) and
(C) and  (D). The numerical method to obtain the height and width of
(D). The numerical method to obtain the height and width of  is described in Figure 9.
is described in Figure 9.References
-
- Gabbiani F, Metzner W, Wessel R, Koch C. From stimulus encoding to feature extraction in weakly electric fish. Nature. 1996;384:564–567. - PubMed
-
- Joris PX, Schreiner CE, Rees A. Neural processing of amplitude-modulated sounds. Physiol Rev. 2004;84:541–577. - PubMed
-
- Bregman AS. Auditory Scene Analysis: The Perceptual Organization of Sounds. Cambridge: MIT Press; 1990. 792
-
- Buschermöhle M, Feudel U, Freund JA. Enhanced signal detectability in comodulated noise introduced by compression. Biol Cybern. 2008;99:491–502. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

