Information processing capacity of dynamical systems
- PMID: 22816038
- PMCID: PMC3400147
- DOI: 10.1038/srep00514
Information processing capacity of dynamical systems
Abstract
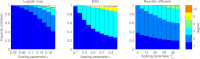
Many dynamical systems, both natural and artificial, are stimulated by time dependent external signals, somehow processing the information contained therein. We demonstrate how to quantify the different modes in which information can be processed by such systems and combine them to define the computational capacity of a dynamical system. This is bounded by the number of linearly independent state variables of the dynamical system, equaling it if the system obeys the fading memory condition. It can be interpreted as the total number of linearly independent functions of its stimuli the system can compute. Our theory combines concepts from machine learning (reservoir computing), system modeling, stochastic processes, and functional analysis. We illustrate our theory by numerical simulations for the logistic map, a recurrent neural network, and a two-dimensional reaction diffusion system, uncovering universal trade-offs between the non-linearity of the computation and the system's short-term memory.
Figures
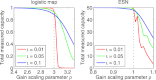

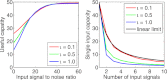
 ). The fraction of the total capacity which is usable increases when the SNR increases, and decreases when the system becomes more non-linear (increasing ι). In the right panel there are a varying number K of i.i.d. inputs with equal power, the total power being kept constant as K varies. The capacity for computing functions of a single input in the presence of multiple inputs is plotted. The black line indicates the situation for a strictly linear system, where the capacity for a single input should equal N/K.
). The fraction of the total capacity which is usable increases when the SNR increases, and decreases when the system becomes more non-linear (increasing ι). In the right panel there are a varying number K of i.i.d. inputs with equal power, the total power being kept constant as K varies. The capacity for computing functions of a single input in the presence of multiple inputs is plotted. The black line indicates the situation for a strictly linear system, where the capacity for a single input should equal N/K.References
-
- Arbib M. (Ed.) The handbook of brain theory and neural networks, second edition. The MIT Press, Cambridge MA (2003).
-
- Maass W., Natschläger T. & Markram H. Real-time computing without stable states: a new framework for neural computation based on perturbations. Neural Comp. 14, 2531–2560 (2002). - PubMed
-
- Jaeger H. & Haas H. Harnessing nonlinearity: predicting chaotic systems and saving energy in wireless communication. Science 304, 78–80 (2004). - PubMed
-
- Verstraeten D., Schrauwen B., D'Haene M. & Stroobandt D. An experimental unification of reservoir computing methods. Neural Networks 20, 391–403 (2007). - PubMed
-
- Vandoorne K. et al. Toward optical signal processing using Photonic Reservoir Computing. Optics Express 16(15), 11182–11192 (2008). - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

