Interactive semiautomatic contour delineation using statistical conditional random fields framework
- PMID: 22830786
- PMCID: PMC3412434
- DOI: 10.1118/1.4728979
Interactive semiautomatic contour delineation using statistical conditional random fields framework
Abstract
Purpose: Contouring a normal anatomical structure during radiation treatment planning requires significant time and effort. The authors present a fast and accurate semiautomatic contour delineation method to reduce the time and effort required of expert users.
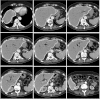
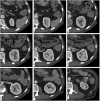
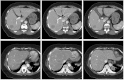
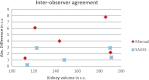
Methods: Following an initial segmentation on one CT slice, the user marks the target organ and nontarget pixels with a few simple brush strokes. The algorithm calculates statistics from this information that, in turn, determines the parameters of an energy function containing both boundary and regional components. The method uses a conditional random field graphical model to define the energy function to be minimized for obtaining an estimated optimal segmentation, and a graph partition algorithm to efficiently solve the energy function minimization. Organ boundary statistics are estimated from the segmentation and propagated to subsequent images; regional statistics are estimated from the simple brush strokes that are either propagated or redrawn as needed on subsequent images. This greatly reduces the user input needed and speeds up segmentations. The proposed method can be further accelerated with graph-based interpolation of alternating slices in place of user-guided segmentation. CT images from phantom and patients were used to evaluate this method. The authors determined the sensitivity and specificity of organ segmentations using physician-drawn contours as ground truth, as well as the predicted-to-ground truth surface distances. Finally, three physicians evaluated the contours for subjective acceptability. Interobserver and intraobserver analysis was also performed and Bland-Altman plots were used to evaluate agreement.
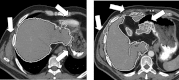
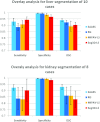
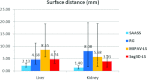
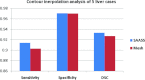
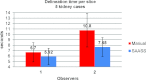
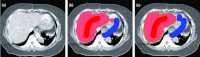
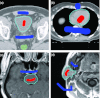
Results: Liver and kidney segmentations in patient volumetric CT images show that boundary samples provided on a single CT slice can be reused through the entire 3D stack of images to obtain accurate segmentation. In liver, our method has better sensitivity and specificity (0.925 and 0.995) than region growing (0.897 and 0.995) and level set methods (0.912 and 0.985) as well as shorter mean predicted-to-ground truth distance (2.13 mm) compared to regional growing (4.58 mm) and level set methods (8.55 mm and 4.74 mm). Similar results are observed in kidney segmentation. Physician evaluation of ten liver cases showed that 83% of contours did not need any modification, while 6% of contours needed modifications as assessed by two or more evaluators. In interobserver and intraobserver analysis, Bland-Altman plots showed our method to have better repeatability than the manual method while the delineation time was 15% faster on average.
Conclusions: Our method achieves high accuracy in liver and kidney segmentation and considerably reduces the time and labor required for contour delineation. Since it extracts purely statistical information from the samples interactively specified by expert users, the method avoids heuristic assumptions commonly used by other methods. In addition, the method can be expanded to 3D directly without modification because the underlying graphical framework and graph partition optimization method fit naturally with the image grid structure.
Figures
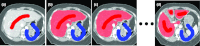
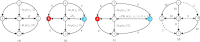
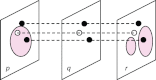
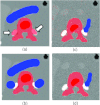

References
-
- Fox J. L., Rosenzweig K. E., Rengan R., O’Meara W., Yorke E., Erdi Y., Nehmeh S., and Leibel S. A., “Does the registration of PET and planning CT images decrease inter-and intra-observer variation in delineating tumor volumes for non-small-cell lung cancer (NSCLC)?,” Int. J. Radiat. Oncol., Biol., Phys. 62, 70–75 (2005).10.1016/j.ijrobp.2004.09.020 - DOI - PubMed
-
- Gao L., Heath D. G., Kuszyk B. S., and Fishman E. K., “Automatic liver segmentation technique for three-dimensional visualization of CT data,” Radiology 201, 359–364 (1996). - PubMed
-
- Adams R. and Bischof L., “Seeded region growing,” IEEE Trans. Pattern Anal. Mach. Intell. 16(6), 641–647 (1994).10.1109/34.295913 - DOI
-
- Pohle R. and Toennies K. D., “Segmentation of medical images using adaptive region growing,” Proc. SPIE Med. Imaging: Image Process. 4322, 1337–1346 (2001).10.1117/12.431013 - DOI
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

