The phylogenetic Kantorovich-Rubinstein metric for environmental sequence samples

Abstract

It is now common to survey microbial communities by sequencing nucleic acid material extracted in bulk from a given environment. Comparative methods are needed that indicate the extent to which two communities differ given data sets of this type. UniFrac, which gives a somewhat ad hoc phylogenetics-based distance between two communities, is one of the most commonly used tools for these analyses. We provide a foundation for such methods by establishing that, if we equate a metagenomic sample with its empirical distribution on a reference phylogenetic tree, then the weighted UniFrac distance between two samples is just the classical Kantorovich-Rubinstein, or earth mover's, distance between the corresponding empirical distributions. We demonstrate that this Kantorovich-Rubinstein distance and extensions incorporating uncertainty in the sample locations can be written as a readily computable integral over the tree, we develop L(p) Zolotarev-type generalizations of the metric, and we show how the p-value of the resulting natural permutation test of the null hypothesis 'no difference between two communities' can be approximated by using a Gaussian process functional. We relate the L(2)-case to an analysis-of-variance type of decomposition, finding that the distribution of its associated Gaussian functional is that of a computable linear combination of independent [Formula: see text] random variables.

Fig. 1

Tree with branches thickened as a linear function of the number of placements in the control sample placed on that branch

Fig. 2

Tree as in Fig. 1, but for the DMSP-treated sample

Fig. 3

Comparison of the distribution of (a) Z₁- and (b) Z₂-distances obtained by shuffling (———), Gaussian approximation (– – –) and the observed value (×) for the example data set

Fig. 4

Dendrogram with barycenters marked: ●, control sample; ★, sample treated with DMSP

Fig. 5

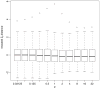
Plot showing sample (○) and randomized ranges ( ): outliers have been eliminated for clarity; for each p, the distribution was rescaled by subtracting the mean and dividing by the standard deviation

Fig. 6

Tree displaying the optimal movement of mass for the KR metric: when moving from the first probability distribution to the second, branches marked in gray have mass moving towards the root, whereas those marked in black have mass moving towards the leaves; thickness shows the quantity of mass moving through that branch