Dynamics of target-mediated drug disposition: characteristic profiles and parameter identification

Abstract

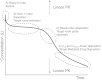
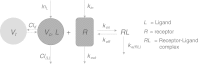
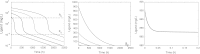
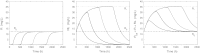
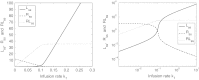
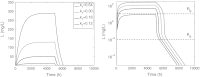
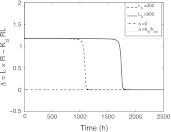
In this paper we present a mathematical analysis of the basic model for target mediated drug disposition (TMDD). Assuming high affinity of ligand to target, we give a qualitative characterisation of ligand versus time graphs for different dosing regimes and derive accurate analytic approximations of different phases in the temporal behaviour of the system. These approximations are used to estimate model parameters, give analytical approximations of such quantities as area under the ligand curve and clearance. We formulate conditions under which a suitably chosen Michaelis-Menten model provides a good approximation of the full TMDD-model over a specified time interval.

Fig. 1

Characteristic ligand versus time graph in target-mediated drug disposition. The concentration of the ligand is measured on a logarithmic scale. In the first phase (A) drug and target rapidly equilibrate, in the second phase (B) the target is saturated and drug is mainly eliminated directly by a first order process, in the third phase (C) the target is no longer saturated and drug is eliminated directly, as well as in the form of a drug–target complex, and in the final, fourth phase (D) the drug concentration is so low that elimination is a linear first order process with direct as well as indirect elimination (as a drug–target complex)

Fig. 2

Schematic description of target-mediated drug (or ligand) disposition. The ligand L binds reversibly (k _on/k _off) to the target R to form the ligand–target complex RL, which is irreversibly removed via a first order rate process (k _e(RL)), and in addition is eliminated via a first order process (k _e(L) = Cl _(L)/V _c)

Fig. 3

Semi-logarithmic graphs of the ligand plasma concentration versus time after the administration of four rapid intravenous injections D of 1.5, 5, 15 and 45 mg/kg, respectively (Data set (I)). The volume of the central compartment V _c for these doses was fixed at 0.05 L/kg. The dots are simulated data and the solid curves are obtained by fitting the model sketched in Fig. 2 to the data. Estimates are given in Table 2

Fig. 4

Left semi-logarithmic graphs of simulated plasma concentrations of L (red discs) and R (blue squares) versus time (Data set (II)) and on the right the same, but also semi-logarithmic graphs of RL (green triangles) (Data set (III)), taken after administration of four rapid intravenous injections D of 1.5, 5, 15 and 45 mg/kg, respectively. V _c for these doses was fixed at 0.05 L/kg. The dots are simulated data and the solid curves are obtained by fitting the model sketched in Fig. 2 to the data. Estimates are given in Table 2

Fig. 5

Graphs of L versus time on semi-logarithmic scale (left), on a linear scale (middle) and a close up (right), for doses resulting in initial ligand concentrations L ₀ = 30, 100, 300, 900 mg/L and parameters listed in Table 3. In addition, R(0) = R ₀ and RL(0) = 0. The dashed lines indicate the target baseline level R ₀, and the dissociation constant K _d

Fig. 6

Graphs of R (left), RL (middle) and R _tot (right) versus time for L ₀ = 30, 100, 300, 900 mg/L and parameters given in Table 3, whilst R(0) = R ₀ and RL(0) = 0. The dashed line indicates the target baseline level R ₀ and the dotted line the level R _*

Fig. 7

Graphs of R ₀ − R (left), RL (middle) and R _tot − R ₀ (right) versus time on a semi-logarithmic scale for L(0) = 30, 100, 300, 900 mg/L and R(0) = R ₀ and RL(0) = 0 mg/L. The parameters are listed in Table 3. In the middle figure, the dashed line indicates the baseline R ₀ and the dotted line the level R _*. In the right figure the dotted line indicates R _* − R ₀

Fig. 8

Graphs of L on a semi-logarithmic scale (left) and R (middle) and RL (right) on a linear scale versus time for L(0) = 0.3, 1, 3, 10, 30, 100, 300, 900 mg/L and R(0) = R ₀ and RL(0) = 0. The parameters are listed in Table 3. The dashed lines indicate the baseline R ₀ and K _d, and the dotted line the level R _*

Fig. 9

Simulated graphs of R _tot(t) for the initial ligand concentrations L ₀ = 30, 100, 300, 900 mg/L and data from Table 3, together with the curve (dashed) given by the analytic expression (20). Notice how, as L ₀ increases, the graph of R _tot(t) follows over a longer period of time

Fig. 10

Graphs of L versus time on a semi-logarithmic scale for data as in Fig. 5. The dashed curves are the analytic approximations for the different drug doses, given by Eq. (25). Recall from Eq. (7) that K _d = 0.011 mg/L

Fig. 11

Fitting the 2-compartment Michaelis–Menten model (45) to the data of Fig. 3 which are represented by the dots. The drawn curves are predictions of the Michaelis–Menten model for the parameter values listed in Table 4. The dashed line in the middle of the plot indicates the estimated value of K _M. Notice how far away it is from the original value of K _m—marked by the thin drawn line—which was estimated by the TMDD model

Fig. 12

The steady state concentrations L _ss, R _ss and RL _ss graphed versus the infusion rate k _f, on a linear scale (left) and on a log-log scale (right) for parameter values taken from Table 3

Fig. 13

The ligand concentration L graphed versus time on a linear scale (left) and on a semi-logarithmic scale (right) for the infusion rates k _f = 0.12, 0.18, 0.30 and 0.54 (mg/L)/h and t _washout = 5000 h. The parameter values are taken from Table 3

Fig. 14

Concentration profiles of R, RL and R _tot versus time caused by a constant rate infusion of 5000 h and infusion rates of k _f = 0.12, 0.18, 0.30 and 0.54 (mg/L)/h. The parameter values are taken from Table 3. Note that the time to full depletion of target R decreases as the infusion rate k _f of ligand increases

Fig. 15

Graphs of R ₀ − R, RL and R _tot − R ₀ versus time when k _f= 0.12, 0.18, 0.30 and 0.54 (mg/L)/h. The parameter values are taken from Table 3. Note that the convergence of target R to R ₀ is bi-exponential and that the decline of complex RL to zero, and the convergence of total target R _tot to R ₀ are mono-exponential

Fig. 16

Schematic representation of how the parameters may be derived from properties of the four phases. In Phase A ligand binds to the receptor (k _on), during Phase B ligand is primarily eliminated directly (k _e(L)); time of termination yields information about k _in. In Phase C the saturation term is important (K _d), and in Phase D ligand elimination proceeds mainly though the receptor (k _e(RL))

Fig. 17

Evolution of the quantity with time for two initial doses L ₀ = 300 and 900. Parameter values are taken from Table 1. Note the agreement with the analytical predictions made above for Phases B, C and D