Synergy and group size in microbial cooperation

Abstract

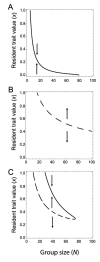
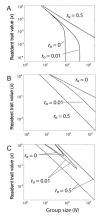
Microbes produce many molecules that are important for their growth and development, and the exploitation of these secretions by nonproducers has recently become an important paradigm in microbial social evolution. Although the production of these public-goods molecules has been studied intensely, little is known of how the benefits accrued and the costs incurred depend on the quantity of public-goods molecules produced. We focus here on the relationship between the shape of the benefit curve and cellular density, using a model assuming three types of benefit functions: diminishing, accelerating, and sigmoidal (accelerating and then diminishing). We classify the latter two as being synergistic and argue that sigmoidal curves are common in microbial systems. Synergistic benefit curves interact with group sizes to give very different expected evolutionary dynamics. In particular, we show that whether and to what extent microbes evolve to produce public goods depends strongly on group size. We show that synergy can create an "evolutionary trap" that can stymie the establishment and maintenance of cooperation. By allowing density-dependent regulation of production (quorum sensing), we show how this trap may be avoided. We discuss the implications of our results on experimental design.

fig 1

Accelerating, decelerating, and sigmoidal benefit functions. A) Total benefit as a function of total public goods investment Nx, expressed as the product of the group size N and the cooperative investment per individual, x. The solid and dashed lines represent synergistic (accelerating) benefits as they have positive concavity for some intervals, whereas the dotted line always represents diminishing returns. B) Corresponding per-capita benefit B(Nx)/N as a function of group size, N, assuming that every individual cooperates at some fixed amount (here, x = 1, meaning full cooperation). The benefit functions used are B(x) = α(β + de^κ–bx)⁻¹ − α(β + de^κ)⁻¹ with α = 10⁵, d = 1, β = 1, κ = 0, and b = 0.1 (decelerating benefits; dotted line), B(x) = bx^a with b = 0.1 and α = 3 (accelerating benefits; dashed line), and α(β +de^κ–bx)⁻¹ − α(β + de^κ)⁻¹ where α = 90000, d = 1, β = 2, κ = 10, b = 0.2. (sigmoidal benefits; solid line).

fig 2

Bifurcation plots illustrating the evolutionary dynamics with decelerating, accelerating, and sigmoidal benefit functions. The solid lines indicate the location of interior singular strategies for different group size N. Arrows indicate the direction of gradual evolution of a monomorphic population. A) Decelerating benefits. There is a unique evolutionarily stable strategy which decreases with group size. When group sizes are greater than approximately 80, cooperation is entirely disfavored. (B(x) = α(β + de^κ–bx)⁻¹) − α(β + de^κ)⁻¹ with α = 2000, d = 1, β = 1, κ = 0, and b = 0.8) B) Accelerating benefits. For small group sizes there is a unique evolutionarily stable strategy corresponding to full defection. As the group size increases, full cooperation also becomes an evolutionarily stable strategy. Any interior singular strategy is repelling and decreases with group size, but never reaches zero. (B(x) = bx^a with b = 0.1 and α = 3) C) Sigmoidal benefits. Up to two interior singular strategies are possible, one repelling and the other attracting. (B(x) = α(β + de^κ–bx)⁻¹ − α(β + de^κ)⁻¹ where α = 10000, d = 1, β = 2, κ = 7, and b = 0.3). Each convergent stable attractor could potentially be an evolutionary branching point. The cost function used is C(x) = cx with c = 5.

fig 3

Evolutionary branching and the emergence of two coexisting strategies of full defection and full cooperation in a setting with sigmoidal benefits and non-linear costs. A) Bifurcation plot illustrating the effects of group size on directional selection for the function used in the other diagrams in the figure. B) A pairwise invasibility plot (PIP) illustrating the monomorphic evolutionary dynamics. There are two singular strategies at approximately x = 0.2 and x = 0.4 of which only the latter is convergence stable. Monomorphic populations with trait values above the first singular strategy will evolve towards the second singular to the singular strategy where they undergo disruptive selection and subsequently evolutionary branching. C) Individual-based simulation demonstrating evolutionary branching at approximately x = 0.4, thus corroborating the predictions from the PIP. The inserted panel shows the evolutionary dynamics for populations which initially have trait values lower than the first singular strategy at approximately x = 0.2; here investment decreases to zero. D) Population dynamics of the resultant coexisting strategies of full defection (x = 0) and full cooperation (x = 1). If the fraction of cooperators is initially below approximately 18%, the cooperators will be eliminated altogether. Otherwise, the population dynamics will result in a stable coexistence with approximately 45% cooperators. The sigmoidal benefit function used is the same as in figure 1, B(x) = b(x³ + βx²)(x² + α)⁻¹, but with different parameters b = 200, β = 450, α = 180. The non-linear cost function used is C(x) = c₁x – c₂x² with c₁ = 170, c₂ = 50. The assumed group size in B-D is N = 30.

fig 4

Effect of assortment (positive relatedness) on the evolutionary dynamics of decelerating, accelerating, and sigmoidal benefit functions. The different curves on each plot correspond to different degrees of others-only relatedness (which are equal to the values of 〈ρ〉): r_o = 0, r_o = 0.01, and r_o = 0.5. Solid lines indicate attracting (convergence-stable) singular strategies, while dashed lines indicate singular strategies which are repelling (not convergence stable). Panels A, B, and C have use all the same benefit and cost functions as in figure 2.

fig 5

Joint evolution of the public goods production trait x and the group-size threshold s, above which the production is expressed. Benefits and costs are as in figure 2C. At each generation, a group is formed of size 5 or size 45 with equal probability. For very low quorum sensing thresholds, production is not affected by changes in group size and evolution inevitably brings the production down to zero. However, for an intermediate range of the quorum sensing threshold s, public goods production can be stably maintained. This is true even if the threshold and production is allowed to co-evolve, provided that initial state is a population with an intermediate quorum sensing threshold and a sufficiently high production. For other initial conditions, co-evolution will bring the production down to zero and increase the threshold to arbitrarily large values.