Absolute risk regression for competing risks: interpretation, link functions, and prediction

Abstract

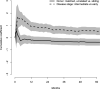
In survival analysis with competing risks, the transformation model allows different functions between the outcome and explanatory variables. However, the model's prediction accuracy and the interpretation of parameters may be sensitive to the choice of link function. We review the practical implications of different link functions for regression of the absolute risk (or cumulative incidence) of an event. Specifically, we consider models in which the regression coefficients β have the following interpretation: The probability of dying from cause D during the next t years changes with a factor exp(β) for a one unit change of the corresponding predictor variable, given fixed values for the other predictor variables. The models have a direct interpretation for the predictive ability of the risk factors. We propose some tools to justify the models in comparison with traditional approaches that combine a series of cause-specific Cox regression models or use the Fine-Gray model. We illustrate the methods with the use of bone marrow transplant data.

Figure 1

A competing risks model describes the time course of subjects that share a common initial state at the time origin (Remission). The time course is terminated when either of the competing events (Event 1: relapse or Event 2: death without relapse) has occurred. The cause-specific hazard functions α₁ and α₂ describe the instantaneous rates of the two events at time t.

Figure 2

Cumulative incidences of events and estimate of follow-up distribution for the BMT study

Figure 3

Time-dependent effects in the absolute risk regression model for relapse. The non-parametric estimates are shown with 95% pointwise confidence intervals.

Figure 4

Predicted cumulative probabilities for the patient status 3 years after the transplant. Compared are the predictions for relapse and death in remission based on absolute risk regression (x-axes) and Fine-Gray regression (y-axes top panels), cause-specific Cox regression (y-axes middle panels), log-odds regression (y-axes bottom panels). Each of the black dots represents the predictions at the predictor values of one patient in the BMT data set.

Figure 5

Prediction error (Brier score) estimated for the predictions for relapse and death in remission based on the same data used for fitting the models (top panels) and based on 1000 steps of bootstrap cross-validation (bottom panels).