Interpreting the widespread nonlinear force spectra of intermolecular bonds

Abstract

Single molecule force spectroscopy probes the strength, lifetime, and energetic details of intermolecular interactions in a simple experiment. A growing number of these studies have reported distinctly nonlinear trends in rupture force with loading rate that are typically explained in conventional models by invoking complex escape pathways. Recent analyses suggested that these trends should be expected even for simple barriers based on the basic assumptions of bond rupture dynamics and thus may represent the norm rather than the exception. Here we explore how these nonlinear trends reflect the two fundamental regimes of bond rupture: (i) a near-equilibrium regime, produced either by bond reforming in the case of a single bond or by asynchronized rupture of multiple individual bonds, and (ii) a kinetic regime produced by fast, non-equilibrium bond rupture. We analyze both single- and multi-bonded cases, describe the full evolution of the system as it transitions between near- and far-from-equilibrium loading regimes, and show that both interpretations produce essentially identical force spectra. Data from 10 different molecular systems show that this model provides a comprehensive description of force spectra for a diverse suite of bonds over experimentally relevant loading rates, removes the inconsistencies of previous interpretations of transition state distances, and gives ready access to both kinetic and thermodynamic information about the interaction. These results imply that single-molecule binding free energies for a vast number of bonds have already been measured.

Fig. 1.

Potential energy profile, two-state kinetics, and comparison of the single-bond model force spectrum to the two-state master equation. (A) 1D energy profile of a single bond (blue curve) loaded by a harmonic potential (dotted green curve). The total potential of the system is represented by the thick black curve. At zero load (I), the harmonic and bond potential minima coincide and a single stable minimum exists. As the harmonic potential is pulled beyond the bond barrier (II) a second minimum is created and the system becomes bistable; however, the barrier impeding rebinding is negligible. Pulling further (III) the re-entry barrier increases and significantly reduces the chance of rebinding. The black dashed line represents the pathway that is commonly assumed beyond the barrier. That is, once the system overcomes the barrier it is carried away irreversibly. (B) Transition rates for unbinding [Eq. 2] and rebinding [Eq. 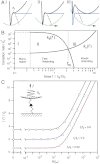3] using typical parameters of , x_t = 1 Å, ΔG_bu = 10 k_BT, and k_c = 100 pN/nm. Rates are in units of and force is in units of k_BT/x_t. The regimes corresponding to stages in the upper panels are partitioned for comparison. (C) The differential equation defining the two-state master equation [Eq. 1] is solved by numerical integration (symbols) with the Bulirsch-Stoer method using Richardson extrapolation (Igor Pro, Wavemetrics). Results are shown for ΔG_bu = 10 k_BT, and three different confinement force values f_k = k_cx_t, which govern the effects of the probing spring constant on the resulting spectrum. The single-bond model in Eq. 6 is calculated with identical parameters for comparison (solid curves).

Fig. 2.

The multi-bond model and comparison to Monte Carlo simulation of N-bonded systems. (A) Schematics of the two limiting pathways when several bonds are allowed to independently unbind and rebind, which are dictated by loading rate. At slow loading, the motion along the N_b coordinate is relatively slow, and rupture occurs once N_b diffusively crosses a threshold defined by a maximum in the free energy (18, 30). At fast loading, the force is quickly raised and thus the drop in N_b will be fast after the initial bond ruptures. In this case the spatial diffusion of one bond over its energy barrier is the slow process which dictates rupture of the cluster. (B) The mean rupture force for the indicated number of N_t bonds, as described by Eq. 7, is solved by the Gillespie algorithm for . 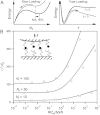Rupture forces for a given trajectory are determined when N_b = 0, and hundreds of trajectories are used to produce the mean rupture force (symbols) plotted here against the dimensionless loading rate. For comparison, the multi-bond model in Eq. 9 is calculated (solid curves) for the same ratio of transition rates, and with .

Fig. 3.

Model fits to the nonlinear force spectra of intermolecular bonds. (A) Force spectrum of the Ni-NTA/His₆ bond measured in this work along with the data of Verbelen et al. (34). Measurements made without Ni²⁺ demonstrate the specificity of the interaction (open circles). Solid lines represent fits to Eq. 6 using identical parameters for both data sets except for the respective spring constants. (B) Force spectra of 10 data sets taken from the literature are fit to Eq. 9 assuming a generic equilibrium force and apparent transition state distance. Data are exploded along the loading rate axis for clarity. Inset: The same force spectra in their raw form illustrating the theoretical range of equilibrium force and cross-over loading rate span (shaded regions). The upward inflection at high forces in the Biotin/Avidin data of ref.  may be due to limited sampling rate effects (41) and enhanced force error at very fast loading rates (42). (C) The same data in B plotted in the natural coordinates of Eq. 9 (see Eq. S3) show that all spectra collapse onto a single line. (D) Biotin-avidin bond rupture data of Teulon et al. (35) are globally fitted to Eq. 9 assuming N = 1, 2, and 3 parallel bonds. 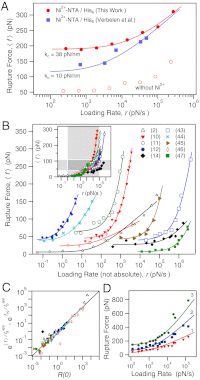Only f_eq is independently fit, while x_t and are shared. Fitted values are x_t = 0.78 Å, , and f_eq = 24.6 pN (N = 1), 58.5 pN (N = 2), 142.3 pN (N = 3). Legend in (B) refers to references and corresponding bonds as follows: Biotin/Avidin (2); LFA-1/ICAM-1 [rest 3A9] (10); Aβ-40/Aβ-40 (11); N,C,N-pincer/pyridine (12); Si₃N₄/Mica in Ethanol (14); peptide/steel (43); Integrin/Fibronectin (; Lysozyme/Anti-Lysozyme (45); Dig/Anti-Dig (46); Actomyosin/ADP (47).