A maximum-likelihood procedure for estimating psychometric functions: thresholds, slopes, and lapses of attention

Abstract

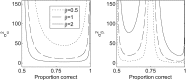
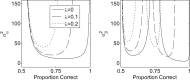
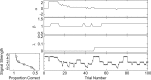
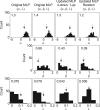
Green [J. Acoust. Soc. Am. 87, 2662-2674 (1990)] suggested an efficient, maximum-likelihood-based approach for adaptively estimating thresholds. Such procedures determine the signal strength on each trial by first identifying the most likely psychometric functions among the pre-proposed alternatives based on responses from previous trials, and then finding the signal strength at the "sweet point" on that most likely function. The sweet point is the point on the psychometric function that is associated with the minimum expected variance. Here, that procedure is extended to reduce poor estimates that result from lapses in attention. The sweet points for the threshold, slope, and lapse parameters of a transformed logistic psychometric function are derived. In addition, alternative stimulus placement algorithms are considered. The result is a relatively fast and robust estimation of a three-parameter psychometric function.

Figure 1

The expected variances of the α (left) and β (right) estimates as a function of the proportion correct for psychometric functions with β values of 0.5 (dotted curves), 1 (dashed curves), and 2 (solid curves). The α, γ, and λ parameters are 0, 0.5, and 0, respectively.

Figure 2

The expected variances of the values of α (left) and β (right) estimates as a function of proportion correct for psychometric functions with λ values of 0.2 (dotted curves), 0.1 (dashed curves), and 0 (solid curves). The α, β, and γ parameters are 0, 1, and 0.5, respectively.

Figure 3

A sample track using a random sweet-point selection rule. Left: the sweet points (circles) on the psychometric function of a virtual observer with α = 0, β = 1, γ = 0.5, and λ = 0.05 (solid curve), and the estimated psychometric function (dashed curve). Right: the maximum-likelihood estimates of α, β, and λ, as well as the signal strength (from top to bottom), in a simulated track that consists of 100 trials.

Figure 4

Same as Fig. 3, except this example is based on a hybrid, 4-down, 1-up sweet-point selection rule.

Figure 5

Histograms of the α (top), β (middle), and λ (bottom) estimates from 100 Monte Carlo simulated procedures using the original maximum-likelihood procedure in which signal strengths are chosen based on just the α-sweet point (first two columns) or based on the updated method that samples four sweet points (last two columns). For the former, the candidate psychometric functions either did (2nd column) or did not (1st column) include the parameter β. For the updated procedures, the four sweet points were either sampled using a 4-down, 1-up algorithm or at random. The number inside each panel indicates the rms error of the estimates relative to the true value. The true psychometric function had parameters α = 2, β = 0.4, γ = 0.5, and λ = 0.1.

Figure 6

As Fig. 5 but the true psychometric function had values of α = 2, β = 1.4, γ = 0.5, and λ = 0.1.

Figure 7

The rms deviations between the parameter estimates and the true parameters of the underlying psychometric function as a function of the number of trials. Changes in the functions indicate the rate at which the parameters converge for three parameters: α, β, and λ (left to right panels). Four procedures were tested: (i) MLP 2D: the original MLP procedure with two parameters, (α, λ); (ii) MLP 3D: the original MLP procedure with two parameters, (α, β, λ); (iii) MLP up-down: the updated MPL procedure a 4-down, 1-up sweet-point selection rules; (iv) MLP random: the updated MLP procedure with random sweet-point selection rule. These are as described for Fig. 5.