Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2013 Mar;27(1):166-77.
doi: 10.1037/a0029508. Epub 2012 Aug 20.

A tutorial on count regression and zero-altered count models for longitudinal substance use data

David C Atkins  1 , Scott A Baldwin, Cheng Zheng, Robert J Gallop, Clayton Neighbors
Affiliations

A tutorial on count regression and zero-altered count models for longitudinal substance use data

David C Atkins et al. Psychol Addict Behav. 2013 Mar.

Erratum in

  • Psychol Addict Behav. 2013 Jun;27(2):379

Abstract

Critical research questions in the study of addictive behaviors concern how these behaviors change over time: either as the result of intervention or in naturalistic settings. The combination of count outcomes that are often strongly skewed with many zeroes (e.g., days using, number of total drinks, number of drinking consequences) with repeated assessments (e.g., longitudinal follow-up after intervention or daily diary data) present challenges for data analyses. The current article provides a tutorial on methods for analyzing longitudinal substance use data, focusing on Poisson, zero-inflated, and hurdle mixed models, which are types of hierarchical or multilevel models. Two example datasets are used throughout, focusing on drinking-related consequences following an intervention and daily drinking over the past 30 days, respectively. Both datasets as well as R, SAS, Mplus, Stata, and SPSS code showing how to fit the models are available on a supplemental website.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Plots of Frequency Counts of Daily Drinks from Timeline Follow-Back (TLFB; upper left) and Rutgers Alcohol Problems Index (RAPI; upper right). Residuals from fitting an ordinary least squares regression to the RAPI or log-transformed RAPI are in lower left and lower right, respectively.
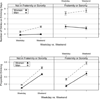
Figure 2
Figure 2
Means and 95% Confidence Intervals for Drinking on Drinking Days (top row) and Proportion of Individuals Drinking (bottom row). Means are stratified by weekend vs. weekday, male vs. female, and fraternity / sorority member or not.
Figure 3
Figure 3
Means and 95% Confidence Intervals for Number of Problems when there are any problems (left) and Proportion of Individuals reporting any drinking-related problems (right). Means are stratified by assessment period and gender.
Figure 4
Figure 4
Plots of frequency counts of data simulated from Poisson distributions with three different means (top row). The bottom row contains frequency counts of data simulated from negative binomial distributions with the same mean but varying dispersion.
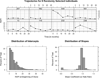
Figure 5
Figure 5
RAPI scores plotted over time for 8 randomly selected individuals (top row). Distribution of intercepts (bottom left) and slopes (bottom right) from fitting separate Poisson regressions to each individual's data.
Figure 6
Figure 6
Predicted (unit-specific) RAPI scores from Poisson GLMM for men and women over time, with specific values noted in text.
Figure 7
Figure 7
Predicted (marginal) drinks for each unique combination of gender, weekend (WE) vs. weekday (WD), and fraternity / sorority status from count submodel of over-dispersed Poisson hurdle mixed model.
See this image and copyright information in PMC

References

    1. Atkins DC, Gallop RJ. Rethinking how family researchers model infrequent outcomes: A tutorial on count regression and zero-inflated models. Journal of Family Psychology. 2007;21:726–735. - PubMed
    1. Bolker BM, Brooks ME, Clark CJ, Geange SW, Poulsen JR, Stevens MHH, White JS. Generalized linear mixed models: A practical guide for ecology and evolution. Trends in Ecology and Evolution. 2009;24(3):127–135. - PubMed
    1. Breslow NE, Clayton DG. Approximate inference in generalized linear mixed models. Journal of the American Statistical Association. 1993;88(421):9–25.
    1. Buntin MB, Zaslavsky AM. Too much ado about two-part models and transformation? Comparing methods of modeling Medicare expenditures. Journal of Health Economics. 2004;23:525–542. - PubMed
    1. Coxe S, West SG, Aiken LS. The analysis of count data: A gentle introduction to Poisson regression and its alternatives. Journal of Personality Assessment. 2009;91:121–136. - PubMed

Publication types