Estimates of acausal joint impedance models

Abstract

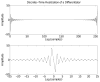
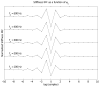
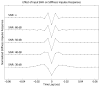
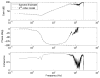
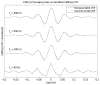
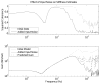
Estimates of joint or limb impedance are commonly used in the study of how the nervous system controls posture and movement, and how that control is altered by injury to the neural or musculoskeletal systems. Impedance characterizes the dynamic relationship between an imposed perturbation of joint position and the torques generated in response. While there are many practical reasons for estimating impedance rather than its inverse, admittance, it is an acausal representation of the limb mechanics that can lead to difficulties in interpretation or use. The purpose of this study was to explore the acausal nature of nonparametric estimates of joint impedance representations to determine how they are influenced by common experimental and computational choices. This was accomplished by deriving discrete-time realizations of first- and second-order derivatives to illustrate two key difficulties in the physical interpretation of impedance impulse response functions. These illustrations were provided using both simulated and experimental data. It was found that the shape of the impedance impulse response depends critically on the selected sampling rate, and on the bandwidth and noise characteristics of the position perturbation used during the estimation process. These results provide important guidelines for designing experiments in which nonparametric estimates of impedance will be obtained, especially when those estimates are to be used in a multistep identification process.

Fig. 1

Simplified block diagram of an experimental apparatus used to study limb dynamics. The Laplace transforms of the measured torque and position are given by T_m (s) and Θ(s), respectively. The input perturbation is applied as the reference input Θ_r (s), and T_v (s) is the torque due to voluntary contractions.

Fig. 2

Discrete-time realization of a differentiator. The upper panel shows the inverse discrete Fourier transform of the function jω. The lower panel shows the periodic extension of the inverse transform, zooming in on the segment near 0 lag. This clearly shows the acausal nature of the IRF, and that it is an odd function. Results were computed for N = 256 points and normalized by removing a factor of ω_s/N.

Fig. 3

Discrete-time realization of a double differentiator. The upper panel shows the inverse discrete Fourier transform of the function −ω². The lower panel shows the periodic extension of the inverse transform, zooming in on the segment near 0 lag, and clearly showing the acausal nature of the IRF. Note that the double-differentiator is an even function. Results were computed for N = 256 points and normalized by removing a factor of ${\omega }_s^2/N^2$.

Fig. 4

Discrete-time impedance IRFs for a second-order system with parameters I = 0.01 N·ms²/rad, B = 0.8 N·ms/rad and K = 140 N·m/rad. These parameters, which are typical values for ankle impedance [22], result in natural frequency and damping parameters of: ω_n = 118 rad/s and ζ = 0.34. The IRFs were normalized by dividing by the square of the sampling frequency, so that the inertial term has the same amplitude in each case.

Fig. 5

The effect of the input bandwidth and SNR on identified impedance IRFs. The system is second-order, and has parameters typical of a human elbow, I = 0.18 N·ms²/rad, B = 1.6 N·ms/rad, K = 62 N·m/rad, resulting in a natural frequency of 18.6 rad/s and relative damping of ζ = 0.24. It was discretized at a sampling frequency of 200 Hz, and then bandlimited using (17), assuming that the input was a white noise signal low-pass filtered at 5 Hz, but contained a small amount of additive white measurement noise (SNR between 30 and 60 dB).

Fig. 6

Parametric fit to a nonparametric impedance transfer function estimate. The upper panel shows the gains of both the spectral transfer function estimate (solid) and a parametric second-order fit (dashed) to that transfer function. The middle panel shows the phase responses of both models. The lower panel shows the estimated squared coherence between the elbow angle and torque. The response approximates a second-order system (I = 0.171 N·ms²/rad, B = 1.22 N·ms/rad and K = 53.5 N·m/rad) below about 20 Hz, whereas the coherence remains near unity up to nearly 50 Hz.

Fig. 7

Parametric and nonparametric impedance impulse responses obtained at various sampling frequencies. All IRFs have been bandlimited to 20 Hz. The nonparametric responses were identified from the same trial used in Fig. 6. The first parametric response (500-Hz sampling) was least-squares fit to the data. The remaining parametric IRFs were generated from the parameters estimated at the 500-Hz sampling rate (I = 0.170 N·ms²/rad, B = 1.67 N·ms/rad and K = 53.7 N·m/rad).

Fig. 8

The effect of input noise on estimated impedance. The top panel shows the squared coherence before (gray) and after (black) the addition of input noise, at a SNR of 25 dB. The lower panel shows the Bode magnitude plots of three impulse response estimates: the system estimated from the initial experimental data (gray), the IRF estimated after the addition of input noise (black), and the transfer function predicted using (17) (dashed).