Meso-scale turbulence in living fluids
- PMID: 22908244
- PMCID: PMC3437854
- DOI: 10.1073/pnas.1202032109
Meso-scale turbulence in living fluids
Abstract
Turbulence is ubiquitous, from oceanic currents to small-scale biological and quantum systems. Self-sustained turbulent motion in microbial suspensions presents an intriguing example of collective dynamical behavior among the simplest forms of life and is important for fluid mixing and molecular transport on the microscale. The mathematical characterization of turbulence phenomena in active nonequilibrium fluids proves even more difficult than for conventional liquids or gases. It is not known which features of turbulent phases in living matter are universal or system-specific or which generalizations of the Navier-Stokes equations are able to describe them adequately. Here, we combine experiments, particle simulations, and continuum theory to identify the statistical properties of self-sustained meso-scale turbulence in active systems. To study how dimensionality and boundary conditions affect collective bacterial dynamics, we measured energy spectra and structure functions in dense Bacillus subtilis suspensions in quasi-2D and 3D geometries. Our experimental results for the bacterial flow statistics agree well with predictions from a minimal model for self-propelled rods, suggesting that at high concentrations the collective motion of the bacteria is dominated by short-range interactions. To provide a basis for future theoretical studies, we propose a minimal continuum model for incompressible bacterial flow. A detailed numerical analysis of the 2D case shows that this theory can reproduce many of the experimentally observed features of self-sustained active turbulence.
Conflict of interest statement
The authors declare no conflict of interest.
Figures


 are approximately Gaussian (thin gray line) for experiments, SPR model, and continuum theory. (B) The distributions of the longitudinal and transverse velocity increments δv‖,⊥, normalized by their first and second moments
are approximately Gaussian (thin gray line) for experiments, SPR model, and continuum theory. (B) The distributions of the longitudinal and transverse velocity increments δv‖,⊥, normalized by their first and second moments  are shown for three different separations R. (C) Longitudinal and transverse velocity structure functions
are shown for three different separations R. (C) Longitudinal and transverse velocity structure functions  normalized by
normalized by  . The maxima of the even transverse structure functions
. The maxima of the even transverse structure functions  reflect the typical vortex size Rv , which is significantly larger in the 3D experiments. Experimental and theoretical data points are spatio-temporal averages over two orthogonal directions in A and B and all directions in C, yielding a typical sample size > 106 per plotted data point in C. Histograms and structure functions for quasi-2D (3D) curves were obtained by combining PIV data from two (15) movies, respectively, representing an average over 2 × 1,000 (15 × 300) frames. Simulation parameters are identical to those in Fig. 2 and summarized in
reflect the typical vortex size Rv , which is significantly larger in the 3D experiments. Experimental and theoretical data points are spatio-temporal averages over two orthogonal directions in A and B and all directions in C, yielding a typical sample size > 106 per plotted data point in C. Histograms and structure functions for quasi-2D (3D) curves were obtained by combining PIV data from two (15) movies, respectively, representing an average over 2 × 1,000 (15 × 300) frames. Simulation parameters are identical to those in Fig. 2 and summarized in 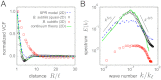
References
-
- Koch DL, Subramanian G. Collective hydrodynamics of swimming microorganisms: Living fluids. Annu Rev Fluid Mech. 2011;43:637–659.
-
- Tero A, et al. Rules for biologically inspired adaptive network design. Science. 2010;327:439–442. - PubMed
-
- Xavier JB, Martinez-Garcia E, Foster KR. Social evolution of spatial patterns in bacterial biofilms: When conflict drives disorder. Am Nat. 2009;174:1–12. - PubMed
-
- Kessler JO, Wojciechowski M. Collective Behavior and Dynamics of Swimming Bacteria. Oxford, UK: Oxford University Press; 1997. pp. 417–450.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

