A canonical model of multistability and scale-invariance in biological systems

Abstract

Multistability and scale-invariant fluctuations occur in a wide variety of biological organisms from bacteria to humans as well as financial, chemical and complex physical systems. Multistability refers to noise driven switches between multiple weakly stable states. Scale-invariant fluctuations arise when there is an approximately constant ratio between the mean and standard deviation of a system's fluctuations. Both are an important property of human perception, movement, decision making and computation and they occur together in the human alpha rhythm, imparting it with complex dynamical behavior. Here, we elucidate their fundamental dynamical mechanisms in a canonical model of nonlinear bifurcations under stochastic fluctuations. We find that the co-occurrence of multistability and scale-invariant fluctuations mandates two important dynamical properties: Multistability arises in the presence of a subcritical Hopf bifurcation, which generates co-existing attractors, whilst the introduction of multiplicative (state-dependent) noise ensures that as the system jumps between these attractors, fluctuations remain in constant proportion to their mean and their temporal statistics become long-tailed. The simple algebraic construction of this model affords a systematic analysis of the contribution of stochastic and nonlinear processes to cortical rhythms, complementing a recently proposed biophysical model. Similar dynamics also occur in a kinetic model of gene regulation, suggesting universality across a broad class of biological phenomena.

Figure 1. Multistability in human EEG data.

A: PDFs derived from long recordings of EEG time series exhibit a low (black) and a high (red) amplitude mode. The overall PDF is well described by their bimodal sum (white). The superiority of the bimodal over the unimodal fit is reflected in the difference of the BIC values (BIC_diff) B: The corresponding dwell times of each mode are well described by stretched exponentials (white). b indicates the dwell time stretched exponential exponent. The gray line indicates a simple exponential form. C: Time series of filtered (8–12 Hz) EEG. D: corresponding power fluctuations of 10 Hz oscillations (color coded according to the crossing of the distributions in panel A).

Figure 2. Varying β for a fixed λ = 4 yields a subcritical Hopf bifurcation.

A: Bifurcation diagram for state parameter β showing the region of bistability. Attracting solutions shown in solid. The unstable repellor (or seperatrix) is shown as the dotted curve. The fixed point loses stability at β = 0. B: The geometry of equation (1) for three different values of β. Attractors are shown as solid diamonds and repellors as open diamonds. Bistability corresponds to the blue setting.

Figure 3. Complete family of Hopf bifurcations.

A: The geometry of equation (1) for different values of the shape parameter λ. B: Corresponding roots of equation (1) (solid: stable; dashed: unstable). As the shape parameter λ increases, the bifurcations morph from supercritical (left) to subcritical (right). Exemplary values of bifurcation parameter β that yield different attractor landscapes are indicated in red (fixed point), blue (coexisting unstable and stable limit cycles) and green (stable limit cycle).

Figure 4. Bistability with purely additive noise for three different values of the bifurcation parameter β.

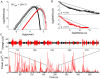
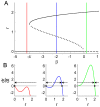
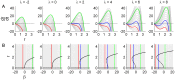
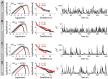
A: Bifurcation diagram for λ = 4. The three values of β used here are indicated in red, blue and green. B: Time course of uncorrelated noise input . C: Phase portraits of example integrations. Black/red indicates inward/outward flow. D: Time series of example integrations. E: Corresponding power PDFs. is the discrete-time analytic signal of r (i.e. the amplitude envelope of r).

Figure 5. Multistability and scale-free fluctuations in the model with both additive and multiplicative noise.

A: Bimodal power PDFs B: Stretched exponential dwell time CDFs for the two modes. C: Time series, showing transitions between low amplitude (black) and high amplitude (red) modes in the model system described by equation (4) with noise parameters η = 45, ρ = 0.61. For additional details please refer to legend of Fig. 1.

Figure 6. Summary system statistics for ‘degree of bimodality’.

A,E: BIC difference between unimodal and bimodal fit; B,F: Relative height of the two modes (abs(0.5-δ)). Dwell-time stretched exponential exponent b, for low (C,G) and high (D,H) energy mode. Left column (panels A–D): System statistics for varying values of the noise parameters η and ρ, with fixed values for the shape parameter λ and bifurcation parameter β. Right column (panels E–H): System statistics for varying values of the shape parameter λ and bifurcation parameter β, with fixed values for the noise parameters η and ρ. White circles indicate the values of the parameters where they are fixed in the complementary panels. Cyan curve indicates theoretical minimum β-value for bistability, showing close agreement with numerical analysis.

Figure 7. Illustration of two EEG data sets and corresponding model solutions.

A: EEG data with frequent high amplitude excursions and short dwelltimes (i.e. less stretched dwelltime CDFs). B: corresponding model solution with ρ = 0.46, η = 30.4. C: EEG data with infrequent high amplitude excursions and long dwelltimes (i.e. more stretched dwelltime CDFs). D: corresponding model solution with ρ = 0.71, η = 57.6.

Figure 8. Two cases of parameter noise in the supercritical setting.

Left column: Small noise variance, right column: Large noise variance. A: Supercritical Hopf bifurcation for λ = −4. The bifurcation parameter β is set to zero and perturbed at each integration time point with a mean reverting stochastic process, see equation (5). Examples of the resulting temporal excursions of β are depicted green. Grey boxes indicate standard deviations of the stochastic process. B: Resulting time-series of . 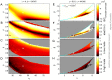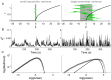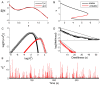C: Corresponding PDF.

Figure 9. Scale-free bimodal fluctuations in a biophysical model of corticothalmic activity.

Results are shown for fluctuating excitatory field potentials φ_e. A: Full family of Hopf bifurcations identified by continuing solutions along a 10 Hz instability. B: Candidate sub-critical Hopf bifurcation (red curve in panel A). Stable attractors in black, unstable solutions in red. C: Candidate Power PDF with clear bimodal distribution. D: Corresponding stretched exponential dwell time CDFs. E: Power time series shows erratic switching.

Figure 10. Bistability and trapping in a kinetic model of genetic regulation.

A: Form of equation (6), f(x) (black), is well matched by best fitting quintic polynomial, g(x) (red). B: Bifurcation diagram of equation (6). C: Candidate Power PDF with clear bimodal distribution. D: Corresponding stretched exponential dwell time CDFs. E: Power time series shows erratic switching.