Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2012 Nov;26(6):816.e21-9.
doi: 10.1016/j.jvoice.2012.04.010. Epub 2012 Aug 24.

Measurement of vocal folds elastic properties for continuum modeling

Fariborz Alipour  1 , Sarah Vigmostad
Affiliations

Measurement of vocal folds elastic properties for continuum modeling

Fariborz Alipour et al. J Voice. 2012 Nov.

Abstract

Objective: This study aimed to quantify the major elastic properties of human vocal fold's lamina propria, including longitudinal and transverse Young's modulus, shear modulus, and Poisson's ratio.

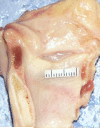
Methods: Samples were obtained from cadaveric human larynges that were snap frozen within 48 hours postmortem and kept at -82°F and thawed overnight in saline solution. Once the sample was tested in the longitudinal direction, two special brackets were glued to the side of each sample and the sample was mounted with brackets in the transverse direction. The shear modulus was obtained from samples mounted between two parallel plates applying shear forces. The Poisson ratio was obtained using high-speed video imaging of two-dimensional samples with markers for longitudinal and transverse strain measurements.

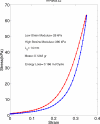
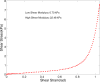
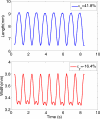
Results: Results indicate that human vocal fold elasticity is very nonlinear with slope that increases 10-15 times from low- to high-strain values. Its average low-strain Young's modulus is approximately 30 kPa in the longitudinal direction and 1 kPa in the transverse direction. The vocal fold longitudinal shear modulus is in the same order of magnitude of its transverse shear modulus (less than 1 kPa). The average Poisson ratio is approximately 0.57.

Conclusions: The present study provides quantitative data for the longitudinal and transverse elastic properties of the human vocal fold tissue and indicates that nonlinear behavior and relative difference of these properties may lead to wide ranges of oscillation frequency and amplitude in human larynges.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Dissected view of a human hemilarynx with millimeter grids over true vocal fold. The false vocal fold is separated from the true fold with a laryngeal ventricle.
Figure 2
Figure 2
Vocal fold samples. A: longitudinal samples with end cartilages and attached sutures; B: sample mounted for transverse experiment; C: sample mounted for shear experiment; D: sample with diamond shape spot for Poisson ratio experiment.
Figure 3
Figure 3
Sample mounting apparatus with temperature controlled bath and adjustable brackets.
Figure 4
Figure 4
Typical force and elongation signals from a human true vocal fold sample. The solid line shows the sample elongation due to the sinusoidal stretch and release at 1-Hz. The dotted line shows the force response of the sample measured with ergometer.
Figure 5
Figure 5
Force-elongation hysteresis loops of a human false vocal fold sample. Sample is stretched in the upper loops and released in the lower loops.
Figure 6
Figure 6
Stress-strain relations of a longitudinal true vocal fold sample averaged from last few relaxed cycles.
Figure 7
Figure 7
Stress-strain relations of a longitudinal false vocal fold sample averaged from last few relaxed cycles.
Figure 8
Figure 8
Stress-strain relations of a transverse true vocal fold sample averaged from last few relaxed cycles.
Figure 9
Figure 9
Shear stress-shear strain relations for true vocal fold sample averaged from last few cycles.
Figure 10
Figure 10
Spot deformation waveforms of a vocal fold sample. The top panel shows the major axis (longitudinal) variation with time and the bottom panel shows the minor axis (transverse) variation. The corresponding strains are displayed in the upper right of each graph.
See this image and copyright information in PMC

References

    1. Alipour F, Berry DA, Titze IR. A finite element model of vocal fold vibration. J Acoust Soc Am. 2000;108:3003–3012. - PubMed
    1. Rosa MO, Pereira JC, Grellet M, Alwan A. A contribution to simulating a three-dimensional larynx model using the finite element method. J Acoust Soc Am. 2003;114(5):2893–2905. - PubMed
    1. Lekhnitskii SG. Theory of Elasticity of an Anisotropic Body. Mir Publisher; Moscow: 1981.
    1. Perlman AL, Titze IR, Cooper DS. Elasticity of Canine Vocal Fold Tissue. J Speech Hear Res. 1984;27(2):212–219. - PubMed
    1. Alipour F, Titze IR. Elastic Models of Vocal Fold Tissues. J Acoust Soc Am. 1991;90(3):1326–1331. - PubMed

Publication types