Functional roles for synaptic-depression within a model of the fly antennal lobe
- PMID: 22927802
- PMCID: PMC3426607
- DOI: 10.1371/journal.pcbi.1002622
Functional roles for synaptic-depression within a model of the fly antennal lobe
Abstract
Several experiments indicate that there exists substantial synaptic-depression at the synapses between olfactory receptor neurons (ORNs) and neurons within the drosophila antenna lobe (AL). This synaptic-depression may be partly caused by vesicle-depletion, and partly caused by presynaptic-inhibition due to the activity of inhibitory local neurons within the AL. While it has been proposed that this synaptic-depression contributes to the nonlinear relationship between ORN and projection neuron (PN) firing-rates, the precise functional role of synaptic-depression at the ORN synapses is not yet fully understood. In this paper we propose two hypotheses linking the information-coding properties of the fly AL with the network mechanisms responsible for ORN-->AL synaptic-depression. Our first hypothesis is related to variance coding of ORN firing-rate information--once stimulation to the ORNs is sufficiently high to saturate glomerular responses, further stimulation of the ORNs increases the regularity of PN spiking activity while maintaining PN firing-rates. The second hypothesis proposes a tradeoff between spike-time reliability and coding-capacity governed by the relative contribution of vesicle-depletion and presynaptic-inhibition to ORN-->AL synaptic-depression. Synaptic-depression caused primarily by vesicle-depletion will give rise to a very reliable system, whereas an equivalent amount of synaptic-depression caused primarily by presynaptic-inhibition will give rise to a less reliable system that is more sensitive to small shifts in odor stimulation. These two hypotheses are substantiated by several small analyzable toy models of the fly AL, as well as a more physiologically realistic large-scale computational model of the fly AL involving 5 glomerular channels.
Conflict of interest statement
The author has declared that no competing interests exist.
Figures
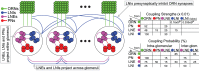
 AL synapses via presynaptic-inhibition. [Right]: The non-negligible connection strengths are listed on top, with the slow-inhibitory connection strengths listed separately from the fast-inhibition strengths. The relevant connection probabilities are listed on the bottom. The parameter
AL synapses via presynaptic-inhibition. [Right]: The non-negligible connection strengths are listed on top, with the slow-inhibitory connection strengths listed separately from the fast-inhibition strengths. The relevant connection probabilities are listed on the bottom. The parameter  refers to
refers to  , which characterizes the overall strength of presynaptic-inhibition. See Methods for full details.
, which characterizes the overall strength of presynaptic-inhibition. See Methods for full details.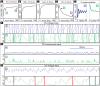
 ’ and ‘
’ and ‘ ’ symbols indicate, respectively, an irregularly firing-regime and a regularly firing-regime. [E] As a result of the fact that the PN conductance has a low variance when the ORN firing-rates are high, the PN activity is very regular when the ORN firing-rate is high. In contrast, the PN activity is less regular when the ORN firing-rate is not as high. This is reflected in the normalized PN autocorrelation, which shows several significant peaks when the variance in the PN conductance is low (‘
’ symbols indicate, respectively, an irregularly firing-regime and a regularly firing-regime. [E] As a result of the fact that the PN conductance has a low variance when the ORN firing-rates are high, the PN activity is very regular when the ORN firing-rate is high. In contrast, the PN activity is less regular when the ORN firing-rate is not as high. This is reflected in the normalized PN autocorrelation, which shows several significant peaks when the variance in the PN conductance is low (‘ ’-regime, left). In contrast, when the variance in the PN conductance is high the autocorrelation does not show significant peaks (‘
’-regime, left). In contrast, when the variance in the PN conductance is high the autocorrelation does not show significant peaks (‘ ’-regime, right). [F] The regularity in the PN spiking activity is seen in PN voltage trace, as shown for the ‘
’-regime, right). [F] The regularity in the PN spiking activity is seen in PN voltage trace, as shown for the ‘ ’-regime (top) and ‘
’-regime (top) and ‘ ’-regime (bottom). [G] The variance in the PN conductance is seen in PN conductance trace, as shown for the ‘
’-regime (bottom). [G] The variance in the PN conductance is seen in PN conductance trace, as shown for the ‘ ’-regime (top) and ‘
’-regime (top) and ‘ ’-regime (bottom). [H] In this panel we show the voltage-trace of a putative Kenyon cell, a conductance-based integrate-and-fire-neuron, driven by either the PN from the
’-regime (bottom). [H] In this panel we show the voltage-trace of a putative Kenyon cell, a conductance-based integrate-and-fire-neuron, driven by either the PN from the  -regime (top) or the PN from the
-regime (top) or the PN from the  -regime (bottom). Thick vertical lines indicate firing-events for this putative KC. When driven by the regular activity of the
-regime (bottom). Thick vertical lines indicate firing-events for this putative KC. When driven by the regular activity of the  -PN, the KC mainains an elevated subthreshold voltage, but does not fire often. On the other hand, when driven by the irregular activity of the
-PN, the KC mainains an elevated subthreshold voltage, but does not fire often. On the other hand, when driven by the irregular activity of the  -PN, the KC does not maintain an elevated subthreshold voltage but fires after each burst in
-PN, the KC does not maintain an elevated subthreshold voltage but fires after each burst in  -PN-activity. This provides a simple illustration of one possible way in a variance-code could be ‘read-out’ by downstream neurons.
-PN-activity. This provides a simple illustration of one possible way in a variance-code could be ‘read-out’ by downstream neurons.
 glomeruli (although to differing degrees). Moreover, we chose every odor within this panel such that the ORN firing-rates of the
glomeruli (although to differing degrees). Moreover, we chose every odor within this panel such that the ORN firing-rates of the  directly stimulated glomeruli were sufficient to saturate the firing-rates of the associated PNs (i.e., the directly stimulated ORN firing-rates were
directly stimulated glomeruli were sufficient to saturate the firing-rates of the associated PNs (i.e., the directly stimulated ORN firing-rates were  12 Hz, see Fig. 10). Given this panel of odors, we presented each odor multiple times, and used the collection of
12 Hz, see Fig. 10). Given this panel of odors, we presented each odor multiple times, and used the collection of  -component PN firing-rate vectors (measured over the
-component PN firing-rate vectors (measured over the  period immediately following odor onset) to perform a variety of odor discrimination tasks (see Results for details). [A] The histogram of discriminability rates associated with
period immediately following odor onset) to perform a variety of odor discrimination tasks (see Results for details). [A] The histogram of discriminability rates associated with  -way discrimination tasks when only firing-rate data is used. Note that
-way discrimination tasks when only firing-rate data is used. Note that  is chance level for these tasks (chance level is also shown in panels B,C,D). [B] The histogram of discriminability rates associated with the
is chance level for these tasks (chance level is also shown in panels B,C,D). [B] The histogram of discriminability rates associated with the  -way discrimination tasks when only firing-rate data is used (note that
-way discrimination tasks when only firing-rate data is used (note that  is chance level for these tasks). [C] The histogram of discriminability rates associated with
is chance level for these tasks). [C] The histogram of discriminability rates associated with  -way discrimination tasks when firing-rate data and
-way discrimination tasks when firing-rate data and  -point correlations (correlation time
-point correlations (correlation time  ) are used. [D] The histogram of discriminability rates associated with
) are used. [D] The histogram of discriminability rates associated with  -way discrimination tasks when firing-rate data and
-way discrimination tasks when firing-rate data and  -point correlations (correlation time
-point correlations (correlation time  ) are used. Note that the typical discriminability rate is higher when correlations are used. [E] Here we plot the difference in mean discriminability for the
) are used. Note that the typical discriminability rate is higher when correlations are used. [E] Here we plot the difference in mean discriminability for the  -way discrimination task between the cases (i) when firing-rate data and
-way discrimination task between the cases (i) when firing-rate data and  -point correlations are used, and (ii) only firing-rate data is used. We plot this difference as a function of the parameters
-point correlations are used, and (ii) only firing-rate data is used. We plot this difference as a function of the parameters  and
and  used in our large-scale model. The vesicle-depletion parameter
used in our large-scale model. The vesicle-depletion parameter  ranges from
ranges from  to
to  across the vertical axis, and the presynaptic-inhibition parameter
across the vertical axis, and the presynaptic-inhibition parameter  ranges from
ranges from  to
to  across the horizontal axis. The data shown in panels A–D is taken from the simulation indicated by the dashed square. Note that, as the total amount of synaptic-depression decreases, the discriminability computed using only firing-rates is closer to the discriminability computed using both firing-rates and
across the horizontal axis. The data shown in panels A–D is taken from the simulation indicated by the dashed square. Note that, as the total amount of synaptic-depression decreases, the discriminability computed using only firing-rates is closer to the discriminability computed using both firing-rates and  -point correlations. [F] Similar to panel-E, except for the
-point correlations. [F] Similar to panel-E, except for the  -way discrimination task, rather than the
-way discrimination task, rather than the  -way discrimination task.
-way discrimination task.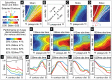
 and
and  (see the section entitled “An illustration of the tradeoff between reliability and sensitivity within a large-scale model” in the main text for details). For each point in this parameter array we measured various features of the network dynamics (such as mean PN spike-counts and reliability), as well as the performance of each of these networks on a
(see the section entitled “An illustration of the tradeoff between reliability and sensitivity within a large-scale model” in the main text for details). For each point in this parameter array we measured various features of the network dynamics (such as mean PN spike-counts and reliability), as well as the performance of each of these networks on a  -way odor discrimination task. [A] Shown is the mean PN spike-count of PNs in the first glomerulus, for each pair of parameter-values
-way odor discrimination task. [A] Shown is the mean PN spike-count of PNs in the first glomerulus, for each pair of parameter-values  ,
,  . Overlaid on top of the mean spike-counts are contour lines for the spike-count. Four of these contours are highlighted in magenta, and will be referenced later. [B] Indications of the type-A and type-B network regimes. [C] Shown are the standard deviation in PN spike-counts of PNs in the first glomerulus (see colorbar on far left). [D] Reproduction of panel-C, along with the contours of panel-A. [E–H] Shown are contour plots associated with
. Overlaid on top of the mean spike-counts are contour lines for the spike-count. Four of these contours are highlighted in magenta, and will be referenced later. [B] Indications of the type-A and type-B network regimes. [C] Shown are the standard deviation in PN spike-counts of PNs in the first glomerulus (see colorbar on far left). [D] Reproduction of panel-C, along with the contours of panel-A. [E–H] Shown are contour plots associated with  for various values of
for various values of  . These panels use the colorbar shown to the far left. [I] Here we plot the standard-deviation in spike-count (taken from panel-D) as a function of the distance along each of the contours indicated in panel-D, with values bi-linearly interpolated as necessary. [J] Here we plot the discriminability values
. These panels use the colorbar shown to the far left. [I] Here we plot the standard-deviation in spike-count (taken from panel-D) as a function of the distance along each of the contours indicated in panel-D, with values bi-linearly interpolated as necessary. [J] Here we plot the discriminability values  indicated in panel-E as a function of the distance along each of the contours shown in panel-D. The contours are indicated using the colorcode from panel-I. [K–M] Similar to panel-J, except for
indicated in panel-E as a function of the distance along each of the contours shown in panel-D. The contours are indicated using the colorcode from panel-I. [K–M] Similar to panel-J, except for  ,
,  , and
, and  respectively.
respectively.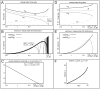
 , and
, and  . In panels A and B the vesicle-depletion parameter
. In panels A and B the vesicle-depletion parameter  . In panels C,D,E and F, the vesicle-depletion parameter
. In panels C,D,E and F, the vesicle-depletion parameter  , such that the mean firing rate
, such that the mean firing rate  is held constant. [A] Graphs of
is held constant. [A] Graphs of  (solid),
(solid),  (dashed),
(dashed),  (gray), and
(gray), and  (gray dashed), as functions of
(gray dashed), as functions of  , for the case
, for the case  . [B] Graphs of var
. [B] Graphs of var (solid) and var
(solid) and var (dashed) as functions of
(dashed) as functions of  , for the case
, for the case  . [C] Graph of
. [C] Graph of  as a function of
as a function of  , subject to the constraint that
, subject to the constraint that  remain constant. The constant value of
remain constant. The constant value of  chosen (essentially arbitrarily) in this case is the value of
chosen (essentially arbitrarily) in this case is the value of  shown in panel A for
shown in panel A for  . Other choices of
. Other choices of  yield similar results. Note that this graph is monotonically decreasing, implying the existence of a 1-parameter family of networks possessing the same
yield similar results. Note that this graph is monotonically decreasing, implying the existence of a 1-parameter family of networks possessing the same  — ranging from type-A networks with low
— ranging from type-A networks with low  and high
and high  , to type-B networks with high
, to type-B networks with high  and low
and low  . [D] Graphs of
. [D] Graphs of  (solid),
(solid),  (dashed),
(dashed),  (gray), and
(gray), and  (gray dashed), for the case
(gray dashed), for the case  . [E] Graphs of var
. [E] Graphs of var (solid) and var
(solid) and var (dashed) as functions of
(dashed) as functions of  , for the case
, for the case  . [F] Graph of the optimal choice of
. [F] Graph of the optimal choice of  (implying a vesicle-depletion parameter of
(implying a vesicle-depletion parameter of  ) for which discriminability is maximized, as a function of the sample number
) for which discriminability is maximized, as a function of the sample number  . The notion of discriminability is described in the section entitled “A simple cartoon of optimizing discriminability over short observation-times”. In this case the observation error
. The notion of discriminability is described in the section entitled “A simple cartoon of optimizing discriminability over short observation-times”. In this case the observation error  is fixed at
is fixed at  . Note that for low
. Note that for low  , discriminability is maximized for a type-B network. However, as
, discriminability is maximized for a type-B network. However, as  increases, discriminability is maximized by type-A networks. The graph shown plots
increases, discriminability is maximized by type-A networks. The graph shown plots  for
for  , as for this particular simple example the derivative of
, as for this particular simple example the derivative of  reaches a vertical asymptote at
reaches a vertical asymptote at  .
.
 ORN-LNI pair is fixed (highlighted in dark gray), whereas the indices
ORN-LNI pair is fixed (highlighted in dark gray), whereas the indices  are not fixed, but are considered distinct from
are not fixed, but are considered distinct from  and from each other. Several dynamic features associated with the
and from each other. Several dynamic features associated with the  LNI can be determined by considering an expansion of the dynamics of this full network in terms of subnetworks. Shown on the right in panels-B,C,D are
LNI can be determined by considering an expansion of the dynamics of this full network in terms of subnetworks. Shown on the right in panels-B,C,D are  -order,
-order,  -order and
-order and  -order subnetworks of the full network which are relevant for determining the sensitivity and reliability of the
-order subnetworks of the full network which are relevant for determining the sensitivity and reliability of the  LNI. The
LNI. The  -order subnetwork consists of the
-order subnetwork consists of the  ORN-LNI pair alone. The two
ORN-LNI pair alone. The two  -order subnetworks shown are those incorporating a single presynaptic-inhibitory connection — namely
-order subnetworks shown are those incorporating a single presynaptic-inhibitory connection — namely  (top) and
(top) and  (bottom). The full network has embedded within it three
(bottom). The full network has embedded within it three  -order subnetworks of the form
-order subnetworks of the form  , and one
, and one  -order subnetwork of the form
-order subnetwork of the form  . The five
. The five  -order subnetworks shown are those incorporating two presynaptic-inhibitory connections. Listed in reading order, these subnetworks are denoted by
-order subnetworks shown are those incorporating two presynaptic-inhibitory connections. Listed in reading order, these subnetworks are denoted by  ,
,  ,
,  ,
,  , and
, and  . The full network has embedded within it
. The full network has embedded within it  ,
,  ,
,  ,
,  and
and  of these subnetworks, respectively.
of these subnetworks, respectively.
 is constant, and the strength of vesicle-depletion
is constant, and the strength of vesicle-depletion  . Note however, that we do not assume that the connectivity
. Note however, that we do not assume that the connectivity  is fixed. We adopt the convention that
is fixed. We adopt the convention that  are distinct indices. [A] Here we illustrate the shift in the ISI-distribution of the
are distinct indices. [A] Here we illustrate the shift in the ISI-distribution of the  LNI (i.e.,
LNI (i.e.,  ) that would occur (up to
) that would occur (up to  -order) if the connectivity
-order) if the connectivity  were increased while decreasing
were increased while decreasing  so as to maintain the firing-rate of the
so as to maintain the firing-rate of the  LNI (denoted by
LNI (denoted by  ). The ISI-distribution of the
). The ISI-distribution of the  LNI when uncoupled from the rest of the network is shown with a dotted-line for reference. The rate at which
LNI when uncoupled from the rest of the network is shown with a dotted-line for reference. The rate at which  changes with respect to an infinitesimal increase in the coupling strength
changes with respect to an infinitesimal increase in the coupling strength  is shown with a dashed-line. This rate is magnified by a factor of
is shown with a dashed-line. This rate is magnified by a factor of  for visibility. The sum of this rate and the uncoupled
for visibility. The sum of this rate and the uncoupled  is shown with a solid-line for a qualitative representation of the new
is shown with a solid-line for a qualitative representation of the new  that would occur if the connectivity
that would occur if the connectivity  were increased by
were increased by  . The inset shows this same data (dotted and solid lines) with time plotted on a logarithmic scale for ease of view. For this particular term in the subnetwork-expansion, as
. The inset shows this same data (dotted and solid lines) with time plotted on a logarithmic scale for ease of view. For this particular term in the subnetwork-expansion, as  increases (and the dotted
increases (and the dotted  shifts to more closely resemble the solid
shifts to more closely resemble the solid  ) the var
) the var increases. The rate at which var
increases. The rate at which var increases as
increases as  is increased is approximately
is increased is approximately  for this system (as indicated by the legend ‘var(ISI)+E-3’). A separate calculation can be performed which shows that the rate at which the sensitivity of the
for this system (as indicated by the legend ‘var(ISI)+E-3’). A separate calculation can be performed which shows that the rate at which the sensitivity of the  LNI (i.e.,
LNI (i.e.,  ) changes as
) changes as  is increased is approximately
is increased is approximately  (as indicted by the legend ‘snstvty+E-2’). Thus, by strengthening the presynaptic-inhibitory connections from several other LNIs onto the
(as indicted by the legend ‘snstvty+E-2’). Thus, by strengthening the presynaptic-inhibitory connections from several other LNIs onto the  ORN-LNI pair (while simultaneously reducing
ORN-LNI pair (while simultaneously reducing  so as to maintain
so as to maintain  ), we can readily show that, to
), we can readily show that, to  -order, these shifts collectively increase both var
-order, these shifts collectively increase both var and the sensitivity
and the sensitivity  . [B–G] In these panels we show similar plots illustrating the influence of various other subnetworks on the reliability of the
. [B–G] In these panels we show similar plots illustrating the influence of various other subnetworks on the reliability of the  LNI. These plots use axes identical to those shown on the inset in panel-A. Listed in reading order, these subnetworks are denoted by
LNI. These plots use axes identical to those shown on the inset in panel-A. Listed in reading order, these subnetworks are denoted by  ,
,  ,
,  ,
,  ,
,  , and
, and  . Note that the contribution of the autapse
. Note that the contribution of the autapse  actually decreases var
actually decreases var , and the contributions of the
, and the contributions of the  -edge subnetworks all decrease the sensitivity
-edge subnetworks all decrease the sensitivity  (albeit with magnitudes that are dwarfed by the contribution of the
(albeit with magnitudes that are dwarfed by the contribution of the  -edge subnetwork
-edge subnetwork  ).
).
 and
and  fixed, one may ask if, for the
fixed, one may ask if, for the  LNI, the reliability of this LNI would decrease if the presynaptic-inhibitory strength
LNI, the reliability of this LNI would decrease if the presynaptic-inhibitory strength  were to be increased (while simultaneously decreasing
were to be increased (while simultaneously decreasing  so as to maintain the firing-rate
so as to maintain the firing-rate  ). Let us denote this condition by ‘hypothesis-2.1’. By analyzing the terms in the
). Let us denote this condition by ‘hypothesis-2.1’. By analyzing the terms in the  -order subnetwork-expansion, one can readily conclude that hypothesis-2.1 holds if the
-order subnetwork-expansion, one can readily conclude that hypothesis-2.1 holds if the  LNI does not presynaptically-inhibit its own ORN, and there is at least one other LNI which does presynaptically-inhibit the
LNI does not presynaptically-inhibit its own ORN, and there is at least one other LNI which does presynaptically-inhibit the  ORN. However, if the
ORN. However, if the  LNI presynaptically-inhibits its own ORN, then hypothesis-2.1 holds only if the size of the network is sufficiently large. This critical network size
LNI presynaptically-inhibits its own ORN, then hypothesis-2.1 holds only if the size of the network is sufficiently large. This critical network size  (above which hypothesis-2.1 holds with high probability) is a function of the background firing-rate of the ORNs
(above which hypothesis-2.1 holds with high probability) is a function of the background firing-rate of the ORNs  , the strength of vesicle-depletion
, the strength of vesicle-depletion  , and the sparsity-coefficient
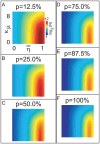
, and the sparsity-coefficient  of the random network. In panel-A we plot
of the random network. In panel-A we plot  , where we have calculated
, where we have calculated  such that, for values of
such that, for values of  , a randomly selected LNI within an E-R random network generated with sparsity-coefficient
, a randomly selected LNI within an E-R random network generated with sparsity-coefficient  is highly likely (probability
is highly likely (probability  75%) to obey hypothesis-2.1, given that the LNI in question presynaptically-inhibits its own ORN. Values of
75%) to obey hypothesis-2.1, given that the LNI in question presynaptically-inhibits its own ORN. Values of  are displayed according to the colorscale shown on the right. In the remaining panels B–F we plot
are displayed according to the colorscale shown on the right. In the remaining panels B–F we plot  for different values of
for different values of  . Note that, unless
. Note that, unless  is small and
is small and  is large, it is highly likely that hypothesis-2.1 holds (even for LNIs which presynaptically-inhibit their own ORNs) for all LNIs within an E-R random network of size
is large, it is highly likely that hypothesis-2.1 holds (even for LNIs which presynaptically-inhibit their own ORNs) for all LNIs within an E-R random network of size  .
.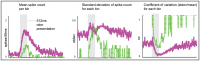
 odor presentation period. Spikes were counted in
odor presentation period. Spikes were counted in  bins. The mean spike-count per
bins. The mean spike-count per  bin (averaged over
bin (averaged over  trials) is shown on the left. The standard-deviation in spike-count per
trials) is shown on the left. The standard-deviation in spike-count per  bin is shown in the center, and the coefficient of variation (standard deviation
bin is shown in the center, and the coefficient of variation (standard deviation mean) is shown on the right. Note that, qualitatively similar to experiment , the model PN activates more quickly, has higher firing-rates, and is more reliable than the ORN.
mean) is shown on the right. Note that, qualitatively similar to experiment , the model PN activates more quickly, has higher firing-rates, and is more reliable than the ORN.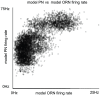
 epoch during which PN firing-rates peak following odor presentation. Note that, qualitatively similar to experiment , the model PN firing-rates saturate for relatively small values of ORN firing-rates.
epoch during which PN firing-rates peak following odor presentation. Note that, qualitatively similar to experiment , the model PN firing-rates saturate for relatively small values of ORN firing-rates.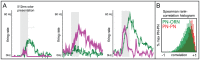
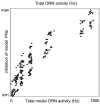
 than the mean of the PN-PN histogram, indicating that, while PNs associated with a given glomerulus tend to respond to the same odors, they do not necessarily respond to the same set of odors which stimulate their associated ORNs.
than the mean of the PN-PN histogram, indicating that, while PNs associated with a given glomerulus tend to respond to the same odors, they do not necessarily respond to the same set of odors which stimulate their associated ORNs.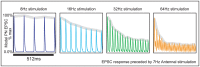
 input current prior to the epoch shown in the figure. At the start of the epoch shown in this figure, the ORN stimulation is increased to
input current prior to the epoch shown in the figure. At the start of the epoch shown in this figure, the ORN stimulation is increased to  ,
,  ,
,  , or
, or  . The trial-averaged model PN EPSCs in response these different stimulations are plotted (over a time interval of
. The trial-averaged model PN EPSCs in response these different stimulations are plotted (over a time interval of  ). Above each EPSC curve, we show the envelope of the response in gray. This envelope is calculated by fitting a piecewise linear function to the maxima of the EPSC response sampled at the rate of stimulation. Note that, similar to experiment, the envelope of the PN EPSC attenuates more quickly when stimulated at
). Above each EPSC curve, we show the envelope of the response in gray. This envelope is calculated by fitting a piecewise linear function to the maxima of the EPSC response sampled at the rate of stimulation. Note that, similar to experiment, the envelope of the PN EPSC attenuates more quickly when stimulated at  than when stimulated at
than when stimulated at  .
.
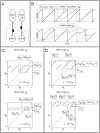
 LNI pairs, each of which presynaptically inhibits the other. [B] Shown on top are sample voltage-traces for the two LNIs (represented by
LNI pairs, each of which presynaptically inhibits the other. [B] Shown on top are sample voltage-traces for the two LNIs (represented by  and
and  ) for the case
) for the case  . Shown on the bottom are sample voltage-traces for the two LNIs in the case that
. Shown on the bottom are sample voltage-traces for the two LNIs in the case that  is nonzero. Note that after LNI A fires,
is nonzero. Note that after LNI A fires,  is constant for
is constant for  -time. Similarly, after LNI B fires
-time. Similarly, after LNI B fires  is constant for
is constant for  -time. A pair of voltages for LNI B are circled. This pair of voltages
-time. A pair of voltages for LNI B are circled. This pair of voltages  corresponds to a point on the graph of the return map
corresponds to a point on the graph of the return map  , namely
, namely  . For this point on the graph of
. For this point on the graph of  ,
,  , and
, and  . [C] Shown on the top and bottom are return maps
. [C] Shown on the top and bottom are return maps  for the values
for the values  , and
, and  , respectively. [D] Shown on the top and bottom are return maps
, respectively. [D] Shown on the top and bottom are return maps  for the values
for the values  , and
, and  , respectively.
, respectively.References
-
- Axel R (1995) The molecular logic of smell. Sci Am 273: 154–159. - PubMed
-
- Hildebrand J, Shepherd G (1997) Mechanisms of olfactory discrimination: converging evidence for common principles across phyla. Annu Rev Neurosci 20: 595–631. - PubMed
-
- Vosshall L, Wong A, Axel R (2000) An olfactory sensory map in the fly brain. Cell 102: 147–159. - PubMed
-
- Gao Q, Yuan Y, Chess A (2000) Convergent projections of Drosophila olfactory neurons to specific glomeruli in the antennal lobe. Nat Neurosci 8: 780–785. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

