Quasi-potential landscape in complex multi-stable systems
- PMID: 22933187
- PMCID: PMC3481575
- DOI: 10.1098/rsif.2012.0434
Quasi-potential landscape in complex multi-stable systems
Abstract
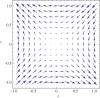
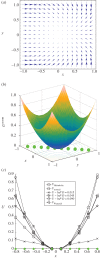
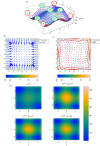
The developmental dynamics of multicellular organisms is a process that takes place in a multi-stable system in which each attractor state represents a cell type, and attractor transitions correspond to cell differentiation paths. This new understanding has revived the idea of a quasi-potential landscape, first proposed by Waddington as a metaphor. To describe development, one is interested in the 'relative stabilities' of N attractors (N > 2). Existing theories of state transition between local minima on some potential landscape deal with the exit part in the transition between two attractors in pair-attractor systems but do not offer the notion of a global potential function that relates more than two attractors to each other. Several ad hoc methods have been used in systems biology to compute a landscape in non-gradient systems, such as gene regulatory networks. Here we present an overview of currently available methods, discuss their limitations and propose a new decomposition of vector fields that permits the computation of a quasi-potential function that is equivalent to the Freidlin-Wentzell potential but is not limited to two attractors. Several examples of decomposition are given, and the significance of such a quasi-potential function is discussed.
Figures
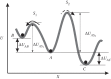
 . Similarly, the transition rate PA→C is not determined by ΔUAC but by
. Similarly, the transition rate PA→C is not determined by ΔUAC but by  .
.
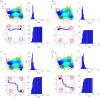
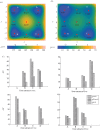
References
-
- Brock A., Chang H., Huang S. 2009. Non-genetic heterogeneity—a mutation-independent driving force for the somatic evolution of tumours. Nat. Rev. Genetics 10, 336–34210.1038/nrg2556 (doi:10.1038/nrg2556) - DOI - DOI - PubMed
-
- Huang S., Kauffman S. 2009. Complex gene regulatory networks—from structure to biological observables: cell fate determination. In Encyclopedia of complexity and systems science (ed. Meyers R. A.). Berlin, Germany: Springer
-
- Nicolis G. 1986. Dissipative systems. Rep. Prog. Phys. 49, 873–94910.1088/0034-4885/49/8/002 (doi:10.1088/0034-4885/49/8/002) - DOI - DOI
-
- Haenggi P., Talkner P., Borkovec M. 1990. Reaction-rate theory: fifty years after Kramers. Rev. Mod. Phys. 62, 251–34110.1103/RevModPhys.62.251 (doi:10.1103/RevModPhys.62.251) - DOI - DOI
-
- Freidlin M. I., Wentzell A. D. 1984. Random perturbations of dynamical systems. Berlin, Germany: Springer
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
