Theory for cross effect dynamic nuclear polarization under magic-angle spinning in solid state nuclear magnetic resonance: the importance of level crossings

Abstract

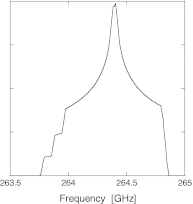
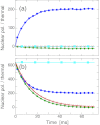
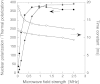
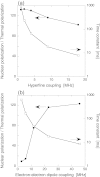
We present theoretical calculations of dynamic nuclear polarization (DNP) due to the cross effect in nuclear magnetic resonance under magic-angle spinning (MAS). Using a three-spin model (two electrons and one nucleus), cross effect DNP with MAS for electron spins with a large g-anisotropy can be seen as a series of spin transitions at avoided crossings of the energy levels, with varying degrees of adiabaticity. If the electron spin-lattice relaxation time T(1e) is large relative to the MAS rotation period, the cross effect can happen as two separate events: (i) partial saturation of one electron spin by the applied microwaves as one electron spin resonance (ESR) frequency crosses the microwave frequency and (ii) flip of all three spins, when the difference of the two ESR frequencies crosses the nuclear frequency, which transfers polarization to the nuclear spin if the two electron spins have different polarizations. In addition, adiabatic level crossings at which the two ESR frequencies become equal serve to maintain non-uniform saturation across the ESR line. We present analytical results based on the Landau-Zener theory of adiabatic transitions, as well as numerical quantum mechanical calculations for the evolution of the time-dependent three-spin system. These calculations provide insight into the dependence of cross effect DNP on various experimental parameters, including MAS frequency, microwave field strength, spin relaxation rates, hyperfine and electron-electron dipole coupling strengths, and the nature of the biradical dopants.

Figure 1

Energy levels of a two-electron, one-nucleus system labeled with approximate z-axis spin states. The central four energy levels are colored to match Fig. 2b.

Figure 2

As a function of the MAS rotor position angle, for one orientation of a nitroxide biradical: (a) ESR frequencies (blue and red lines) with microwave frequency indicated by dashed line; (b) central four energy levels of the three-spin system, colored to match Fig. 1; (c) electron and nuclear polarization from density matrix calculations during the first rotor period with hyperfine coupling, after equilibration of microwaves and electrons for 5T_1e. Parameters used for the calculations are listed in Table 1. Three types of energy level avoided crossings are circled in parts (a) and (b): (1) ESR frequency crosses microwave frequency; (2) ESR frequency difference crosses NMR frequency; (3) ESR frequencies cross. The inset of part (b) shows an expanded view of the last avoided crossing of the rotor period. For part (c), 100 sets of random T_2e fields were averaged.

Figure 3

Nitroxide powder pattern lineshape used for calculations, shown at 9.4 T. The electron g-tensor principal values are 2.0061, 2.0021, 2.0094. The ¹⁴N hyperfine coupling principal values are 18.8, 92.4, 18.2 MHz, for the x, y, and z axes, respectively.

Figure 4

Time dependence of nuclear spin polarization for four different biradical orientations for (a) nuclear spin polarization starting at thermal polarization and (b) nuclear spin polarization starting at thermal electron spin polarization. In these simulations, the hyperfine coupling (h_zz,max) and the nuclear spin-lattice relaxation are not included for 5T_1e (10 ms), then turned on at time 0 to initiate DNP. Level crossings for each orientation: blue circles, both electron-microwave and three-spin crossings (shown in Fig. 2); light blue squares, no three-spin crossing; red crosses, no electron-microwave crossing, but has three-spin crossing; green diamonds, electron-microwave crossing for higher frequency electron. 100 sets of random T_2e fields were averaged. For clarity, only some of the data points are shown.

Figure 5

Steady-state nuclear spin polarizations (as a ratio to thermal polarization) (n_pol,ss) and time constants (t_DNP) for 787 of 1000 random biradical orientations. The remaining 213 orientations are not shown because their values of t_DNP exceeded 100 ms.

Figure 6

Average steady-state nuclear spin polarization (n_pol,av, solid symbols) and time constant (t_DNP,av, open symbols) as a function of microwave field strength (ω₁/2π) for T_1e = 2 ms (circles) and T_1e = 0.2 ms (diamonds). Lines are drawn to guide the eye.

Figure 7

Average steady-state nuclear spin polarization (n_pol,av, solid symbols) and time constant (t_DNP,av, open symbols) as a function of (a) hyperfine coupling (h_zz,max/2π) and (b) electron-electron dipole coupling (d_max/2π). 100 biradical orientations are calculated for 1.4 s (10⁴ × t_r). Lines are drawn to guide the eye.

Figure 8

(a) Average steady-state nuclear spin polarization (n_pol,av) and (b) time constant (t_DNP,av), as a function of MAS frequency (ω_r/2π) for simulations with ω₁/2π = 0.08 MHz and T_1e = 2 ms (circles), with ω₁/2π = 0.8 MHz and T_1e = 2 ms (squares), and with ω₁/2π = 0.8 MHz and T_1e = 0.2 ms (diamonds). 100 biradical orientations were used for the powder average and the calculations were run for 71 ms or longer. MAS frequencies below 210 Hz were calculated with a 10 ns timestep. Lines are drawn to guide the eye.

Figure 9

Average steady-state nuclear spin polarization (n_pol,av, solid symbols) and time constant (t_DNP,av, open symbols) as a function of microwave frequency (ω_m/2π) for (a) a Totapol biradical and (b) a hypothetical narrow-line biradical, composed of two radicals with different g-factors (both with 30 MHz axially symmetric g-anisotropy), so that the ESR frequencies are separated by ω_n. Lines are drawn to guide the eye.

Figure 10

Dependence of the average steady-state nuclear spin polarization (n_pol,av, solid symbols) and time constant (t_DNP,av, open symbols) on magnetic field for microwave field strengths (ω₁/2π) of 2 MHz (circles) and 80 kHz (diamonds). Calculations were performed for ¹H NMR frequencies of 400.9, 600.0, and 800.0 MHz, with ω_m/2π equal to 264.0, 395.1, and 526.8 GHz, respectively (corresponding to the maximum positive DNP enhancements). The calculations were run for 2000 × t_r (286 ms). Lines are drawn to guide the eye.