An Information Theory Approach to Nonlinear, Nonequilibrium Thermodynamics

Abstract

Using the problem of ion channel thermodynamics as an example, we illustrate the idea of building up complex thermodynamic models by successively adding physical information. We present a new formulation of information algebra that generalizes methods of both information theory and statistical mechanics. From this foundation we derive a theory for ion channel kinetics, identifying a nonequilibrium 'process' free energy functional in addition to the well-known integrated work functionals. The Gibbs-Maxwell relation for the free energy functional is a Green-Kubo relation, applicable arbitrarily far from equilibrium, that captures the effect of non-local and time-dependent behavior from transient thermal and mechanical driving forces. Comparing the physical significance of the Lagrange multipliers to the canonical ensemble suggests definitions of nonequilibrium ensembles at constant capacitance or inductance in addition to constant resistance. Our result is that statistical mechanical descriptions derived from a few primitive algebraic operations on information can be used to create experimentally-relevant and computable models. By construction, these models may use information from more detailed atomistic simulations. Two surprising consequences to be explored in further work are that (in)distinguishability factors are automatically predicted from the problem formulation and that a direct analogue of the second law for thermodynamic entropy production is found by considering information loss in stochastic processes. The information loss identifies a novel contribution from the instantaneous information entropy that ensures non-negative loss.

Fig. 1

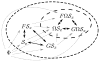
Reaction diagram showing system states as nodes. Two constraints, , defining a coordinate space, and Ω, defining some further restriction are illustrated here. F and G are average value constraints, and their relative likelihoods can be calculated using (9) in either direction. For identical constraints, all hypotheses are completely connected, as shown by the double-headed, dark arrows. Restrictions such as or Ω limit the set of propositions that can be directly compared without knowledge of P(Ω|I)/P(Φ|I), and only one comparison direction is allowed, illustrated by the grey, dotted arrows

Fig. 2

KcsA ion channel selectivity filter in its biological orientation (intracellular solution below) showing ion binding sites S₁–S₄. For visual clarity, two of the four identical monomer units are not shown. Physiological conventions for the potential difference, ΔV, and direction of outward positive current (g) are indicated. Also shown are sites left unoccupied in channel conformations I₁ (S₂ unoccupied) and I₂ (S₂, S₃ unoccupied)

Fig. 3

Ion occupancy distribution in successively complex models. Number distributions are plotted normally (right scale), while probabilities for occupancy of individual sites are plotted vertically (top scale). The set of figures on the left do not include protein conformational changes, while those on the right include the possibility of pinching at S₂ or both S₂ and S₃. The models are (from top to bottom), the default uniform distribution, a simple electrostatic energy distribution, a model based on the free energies of Ref. [29], and a nonequilibrium simulation using the same free energies

Fig. 4

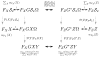
Reaction diagram for adding conditional maximum entropy information. Partition functions, determined by likelihood ratios for each transition, are written out for each state. For the ‘forward’ process F_X → F_X G Ω, there is a ‘reverse’ process F_Z → F_Z G^* Ω signifying the dual maximum conditional entropy problem

Fig. 5

Current-voltage plot calculated using the free energies from Fig. 2 of Ref. [29] along with the assumptions listed in the text. The voltage plotted in this figure is the sum of the five voltage steps between S₀–S₅. Traces are labeled using internal/external cation concentrations (in mM). The integrated autocorrelation function is shown along with its tangent lines according to (33). The reversal potential shifts are physically reasonable, and inward rectification is observed