Evolution of cooperation driven by zealots
- PMID: 22966421
- PMCID: PMC3437515
- DOI: 10.1038/srep00646
Evolution of cooperation driven by zealots
Abstract
Recent experimental results with humans involved in social dilemma games suggest that cooperation may be a contagious phenomenon and that the selection pressure operating on evolutionary dynamics (i.e., mimicry) is relatively weak. I propose an evolutionary dynamics model that links these experimental findings and evolution of cooperation. By assuming a small fraction of (imperfect) zealous cooperators, I show that a large fraction of cooperation emerges in evolutionary dynamics of social dilemma games. Even if defection is more lucrative than cooperation for most individuals, they often mimic cooperation of fellows unless the selection pressure is very strong. Then, zealous cooperators can transform the population to be even fully cooperative under standard evolutionary dynamics.
Conflict of interest statement
The author declares no competing financial interests.
Figures
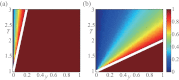
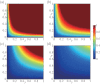
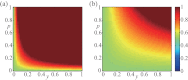
 . (a) T = 1.5. (b) T = 2.5.
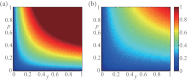
. (a) T = 1.5. (b) T = 2.5.
Similar articles
-
Zealous cooperation does not always promote cooperation in public goods games.Chaos. 2023 Jun 1;33(6):063111. doi: 10.1063/5.0138258. Chaos. 2023. PMID: 37276560
-
Eco-evolutionary feedback and the invasion of cooperation in prisoner's dilemma games.PLoS One. 2011;6(11):e27523. doi: 10.1371/journal.pone.0027523. Epub 2011 Nov 18. PLoS One. 2011. PMID: 22125615 Free PMC article.
-
Sequential interactions-in which one player plays first and another responds-promote cooperation in evolutionary-dynamical simulations of single-shot Prisoner's Dilemma and Snowdrift games.J Theor Biol. 2018 Sep 7;452:69-80. doi: 10.1016/j.jtbi.2018.05.007. Epub 2018 May 21. J Theor Biol. 2018. PMID: 29763610
-
Coevolutionary games--a mini review.Biosystems. 2010 Feb;99(2):109-25. doi: 10.1016/j.biosystems.2009.10.003. Epub 2009 Oct 29. Biosystems. 2010. PMID: 19837129 Review.
-
Evolutionary dynamics in structured populations.Philos Trans R Soc Lond B Biol Sci. 2010 Jan 12;365(1537):19-30. doi: 10.1098/rstb.2009.0215. Philos Trans R Soc Lond B Biol Sci. 2010. PMID: 20008382 Free PMC article. Review.
Cited by
-
Beyond a binary theorizing of prosociality.Proc Natl Acad Sci U S A. 2024 Dec 3;121(49):e2412195121. doi: 10.1073/pnas.2412195121. Epub 2024 Nov 27. Proc Natl Acad Sci U S A. 2024. PMID: 39602256 Free PMC article.
-
Reaching Consensus by Allowing Moments of Indecision.Sci Rep. 2015 Oct 6;5:14839. doi: 10.1038/srep14839. Sci Rep. 2015. PMID: 26439503 Free PMC article.
-
Players acting as leaders in turn improve cooperation.R Soc Open Sci. 2019 Jul 10;6(7):190251. doi: 10.1098/rsos.190251. eCollection 2019 Jul. R Soc Open Sci. 2019. PMID: 31417730 Free PMC article.
-
Network Engineering Using Autonomous Agents Increases Cooperation in Human Groups.iScience. 2020 Aug 6;23(9):101438. doi: 10.1016/j.isci.2020.101438. Online ahead of print. iScience. 2020. PMID: 32823053 Free PMC article.
-
Role of committed minorities in times of crisis.Sci Rep. 2013;3:1371. doi: 10.1038/srep01371. Sci Rep. 2013. PMID: 23455718 Free PMC article.
References
-
- Nowak M. A. Evolutionary Dynamics (The Belknap Press of Harvard University Press, MA, 2006).
-
- Yamagishi T. & Cook K. S. Generalized exchange and social dilemmas. Social Psychology Quarterly 56, 235–248 (1993).
-
- Molm L. D., Collett J. L. & Schaefer D. R. Building solidarity through generalized exchange: a theory of reciprocity. Am. J. Sociol. 113, 205–242 (2007).
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

