Parameter-free model discrimination criterion based on steady-state coplanarity

Abstract

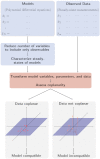
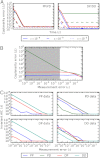
We introduce a procedure for deciding when a mass-action model is incompatible with observed steady-state data that does not require any parameter estimation. Thus, we avoid the difficulties of nonlinear optimization typically associated with methods based on parameter fitting. Instead, we borrow ideas from algebraic geometry to construct a transformation of the model variables such that any set of steady states of the model under that transformation lies on a common plane, irrespective of the values of the model parameters. Model rejection can then be performed by assessing the degree to which the transformed data deviate from coplanarity. We demonstrate our method by applying it to models of multisite phosphorylation and cell death signaling. Our framework offers a parameter-free perspective on the statistical model selection problem, which can complement conventional statistical methods in certain classes of problems where inference has to be based on steady-state data and the model structures allow for suitable algebraic relationships among the steady-state solutions.

Fig. 1.

Parameter-free method for model discrimination.

Fig. 2.

Discrimination of multisite phosphorylation models. (A) Coplanarity error Δ of the steady-state invariants of the PP/PD (Left) and DP/DD (Right) models along time course trajectories simulated from the PP model, corrupted by various levels of noise (lined, ϵ = 10^-9; dashed, ϵ = 10^-6; dotted, ϵ = 10^-3). At each noise level, the errors for three invariants are shown (blue, I₁; green, I₂; red, I₃). (B) Coplanarity error Δ of DP/DD invariants on PP data at steady state as a function of the noise level ϵ; invariants colored as in A. The shaded region indicates the regime over which the DP/DD models can be rejected at significance level α = 0.05. (C) Invariant error AIC A for each model (blue, PP; green, PD; red, DP; cyan, DD) on data generated from the PP (Upper Left), PD (Upper Right), DP (Lower Left), and DD (Lower Right) models.

Fig. 3.

Discrimination of cell death signaling models. (A) Coplanarity error Δ of the steady-state invariants of the cross-linking (Left) and cluster (Right) models along time course trajectories simulated from the cluster model, corrupted by various levels of noise (blue, ϵ = 10^-9; green, ϵ = 10^-6; red, ϵ = 10^-3). (B) Coplanarity error Δ of model invariants (blue, cross-linking; green, cluster) on cluster data at steady state as a function of the noise level ϵ. The shaded region indicates the regime over which the cross-linking model can be rejected at significance level α = 0.05. (C) Invariant error AIC A for each model (blue, cross-linking; green, cluster) on data generated from the cross-linking (Left) and cluster (Right) models.