Fusimotor control of spindle sensitivity regulates central and peripheral coding of joint angles

Abstract

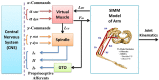
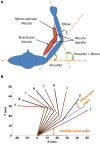
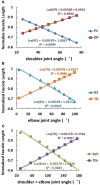
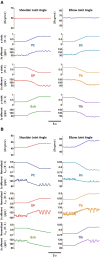
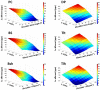
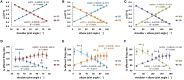
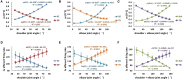
Proprioceptive afferents from muscle spindles encode information about peripheral joint movements for the central nervous system (CNS). The sensitivity of muscle spindle is nonlinearly dependent on the activation of gamma (γ) motoneurons in the spinal cord that receives inputs from the motor cortex. How fusimotor control of spindle sensitivity affects proprioceptive coding of joint position is not clear. Furthermore, what information is carried in the fusimotor signal from the motor cortex to the muscle spindle is largely unknown. In this study, we addressed the issue of communication between the central and peripheral sensorimotor systems using a computational approach based on the virtual arm (VA) model. In simulation experiments within the operational range of joint movements, the gamma static commands (γ(s)) to the spindles of both mono-articular and bi-articular muscles were hypothesized (1) to remain constant, (2) to be modulated with joint angles linearly, and (3) to be modulated with joint angles nonlinearly. Simulation results revealed a nonlinear landscape of Ia afferent with respect to both γ(s) activation and joint angle. Among the three hypotheses, the constant and linear strategies did not yield Ia responses that matched the experimental data, and therefore, were rejected as plausible strategies of spindle sensitivity control. However, if γ(s) commands were quadratically modulated with joint angles, a robust linear relation between Ia afferents and joint angles could be obtained in both mono-articular and bi-articular muscles. With the quadratic strategy of spindle sensitivity control, γ(s) commands may serve as the CNS outputs that inform the periphery of central coding of joint angles. The results suggest that the information of joint angles may be communicated between the CNS and muscles via the descending γ(s) efferent and Ia afferent signals.

Keywords: Ia afferents; central and peripheral coding; joint angle; muscle spindle; spindle sensitivity; γs control.

Figure 1

The virtual arm (VA) model is an integrated neuromuscular sensorimotor systems model in SIMULINK, which encompasses an anatomically accurate structure of upper arm, physiologically realistic muscle mechanics and dynamics, and spindle and Golgi tendon organ (GTO) proprioceptors. Each subcomponent embodies a set of mathematical equations obtained from previous experimental data in literature that describe the physiological, geometrical, kinematic, and dynamic properties of the subsystems. The VA model receives α and γ commands from the central nervous system (CNS), and outputs numerical results of simulation for all state variables, including joint kinematics and proprioceptive afferents (i.e., Ia, Ib, and II afferents). The biomechanical model of the VA has two degrees of freedom (DOFs) in horizontal plane (shoulder flexion/extension, elbow flexion/extension) and is driven by six muscles, which are clavicle portion of pectorailis major (PC) and deltoid posterior (DP) for shoulder joint, brachialis (BS) and triceps lateral head (Tlt) for elbow joint, and biceps short head (Bsh) and tricps long head (Tlh) cross both joints. The virtual muscle (VM) model activated by commands calculates contraction forces (F_m) and instantaneous muscle fascicle length (L_ce). The muscle spindle model receives inputs of fascicle length (L_ce) and fusimotor modulation (γ_s, γ_d) and generates primary (la) and secondary (II) afferents. However, since we are interested in neural coding for joint angles in this study, only γ_s and Ia afferent signal is of interest in the simulation and analysis.

Figure 2

(A) Geometric definition of shoulder and elbow angles. The range of shoulder flexion is set from 0° (fully extended) to 120° (fully flexed), and the range of elbow flexion is from 0° (fully extended) to 150° (fully flexed). Showing in the figure are a typical mono-articular muscle crossing the elbow joint, and a typical bi-articular muscle crossing both shoulder and elbow joints. The spindles are arranged in parallel with muscle fascicle fibers. We hypothesize that muscle fascicle length (L_ce) and Ia afferent are related to the corresponding joint angles of span. Thus for bi-articular muscles, they are related to the sum of joint angles of span. (B) Nine sets of α_stat commands (Table 1) are used to stabilize the VA model at nine equilibrium positions (1 ~ 9) in horizontal plane, respectively. At each position the spindle sensitivity control by γ_stat is investigated.

Figure 3

Relation between equilibrium joint angle and muscle fascicle length (θ_EP − L_ce)of each muscle obtained in the range of joint angles used in simulation. (A) Relation of shoulder mono-articular muscles PC and DP. (B) Relation of elbow mono-articular muscles BS and Tlt. (C) Relation of bi-articular muscles Bsh and Tlh cross both shoulder and elbow joints. Results indicate that a nearly linear relation exists between muscle fibre length and joint angle for both mono-articular muscles and bi-articular muscles, because of the their arrangement. The fascicle length of flexor is shortened and that of extensor is lengthened with increase of the joint angles of span. For bi-articular muscles Bsh and Tlh, their fascicle length, L_ce, is found linearly related to the sum of shoulder and elbow angles. The linearity in the geometric relations provides supportive evidence for a simple coding relationship between joint angles and spindle input and output that are related to muscle fascicle length.

Figure 4

Responses of primary afferents (Ia) of muscle spindles to (A) ramped γ_s drive, and (B) ramped joint angle (fascicle length) change, respectively. (A) The VA was maintained at position 5, while γ_s commands of flexors ramped from 0.3 up to 0.8 and those of extensors ramped from 0.7 down to 0.2, concurrently within 5 s. The Ia afferents of all muscles were shown to be modulated in-phase with γ_s changes. (B) The VA was moved from position 4 to 6 within 5 s by ramped alpha commands of single joint muscles, while the γ_s commands of each muscle remained constant at 0.5. The muscle fascicle length changed simultaneously with joint angles, and the Ia afferents were modulated in-phase with changes in fascicle length L_ce. These demonstrate the sensitivity Ia afferents with respect to fusimotor activation γ_s and muscle fascicle length L_ce.

Figure 5

The landscape of Ia afferent sensitivity with respect to the full ranges of fusimotor commands and muscle fascicle lengths (θ_EP − γ_s - Ia). This is obtained by increasing fusimotor drive at each joint angle for all muscles incrementally. The sensitivity landscapes clearly reveal the complex interrelations of Ia afferents with both fusimotor control and joint angles. In general, the interrelation is nonlinear, and the nonlinearity is more prominent at the lower and higher values of fusimotor commands and joint angles. These nonlinearities may be due to sluggish sensitivity in the short fascicle length and saturation in the long fascicle length. However, it is also clear that the nonlinearity exists in the middle range of fusimotor commands for all muscles. This phenomenon reflects the nonlinear nature of physiological responses of muscle spindles.

Figure 6

The constant fusimotor control strategy, θ_EP − γ_s, curves (A–C), and Ia afferents response (θ_EP − Ia) curves of muscle spindles (D–F), for each muscle. The (A,D) is for shoulder actuators, the (B,E) is for elbow actuators, and the (C,F) is for bi-articular muscles. The abscissas indicate joint flexion angles while the vertical axis indicate activation levels (A–C) or firing rates (D–F). The γ_s inputs of muscle spindles are set to medium constant levels at different angular positions, the firing rates of Ia afferents show an excellent linear relation with joint angles (with a goodness of fitting R² > 0.99). This result may be evident from the sensitivity landscape of Figure 5, from which a constant γ_s value results in a fairly linear (θ_EP − Ia) relation.

Figure 7

The linear fusimotor control strategy, θ_EP − γ_s curves (A–C), and Ia afferents response, (θ_EP − Ia) curves of muscle spindles (D–F), for all muscles. The (A,D) is for shoulder actuators, the (B,E) is for elbow actuators, and the (C,F) is for bi-articular muscles. The axes were defined the same as in Figure 6. When γ_s inputs of muscle spindles are linearly modulated with joint angles from 0.3 to 0.9, the firing rates of Ia afferents do not display a linear and monotonical relation to joint angles. Saturations of Ia responses occur at each muscle, as indicated by the arrows. This is due to the nonlinear physiological properties of muscle spindle demonstrated in Figure 5, and would not be possible to avoid if the full range of fusimotor commands were to be used to encode joint angle information.

Figure 8

The quadratic strategy of fusimotor control, θ_EP − γ_s curves (A–C), and Ia afferents response, (θ_EP − Ia) curves of muscle spindles (D–F), for each muscle. The (A,D) is for shoulder actuators, the (B,E) is for elbow actuators, and the (C,F) is for bi-articular muscles. The axes were defined the same as in Figure 6. When γ_s inputs of muscle spindles are modulated with joint angles θ_EP quadratically in a monotonical manner with joint angles from 0.3 to 0.9, the firing rates of Ia afferents show a robust linear relation with joint angles with an average goodness of linear fitting R² > 0.99. This phenomenon suggests that it is possible to manipulate the fusimotor commands to linearize the nonlinear Ia sensitivity revealed in Figure 5.