An imaging-based stochastic model for simulation of tumour vasculature
- PMID: 22971525
- PMCID: PMC3574631
- DOI: 10.1088/0031-9155/57/19/6103
An imaging-based stochastic model for simulation of tumour vasculature
Abstract
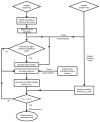
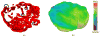
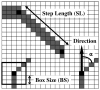
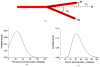
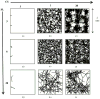
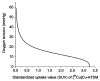
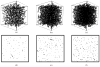
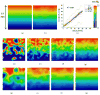
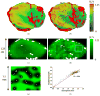
A mathematical model which reconstructs the structure of existing vasculature using patient-specific anatomical, functional and molecular imaging as input was developed. The vessel structure is modelled according to empirical vascular parameters, such as the mean vessel branching angle. The model is calibrated such that the resultant oxygen map modelled from the simulated microvasculature stochastically matches the input oxygen map to a high degree of accuracy (R(2) ≈ 1). The calibrated model was successfully applied to preclinical imaging data. Starting from the anatomical vasculature image (obtained from contrast-enhanced computed tomography), a representative map of the complete vasculature was stochastically simulated as determined by the oxygen map (obtained from hypoxia [(64)Cu]Cu-ATSM positron emission tomography). The simulated microscopic vasculature and the calculated oxygenation map successfully represent the imaged hypoxia distribution (R(2) = 0.94). The model elicits the parameters required to simulate vasculature consistent with imaging and provides a key mathematical relationship relating the vessel volume to the tissue oxygen tension. Apart from providing an excellent framework for visualizing the imaging gap between the microscopic and macroscopic imagings, the model has the potential to be extended as a tool to study the dynamics between the tumour and the vasculature in a patient-specific manner and has an application in the simulation of anti-angiogenic therapies.
Figures

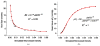
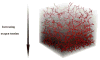
References
-
- Anderson A, Chaplain M. Continuous and discrete mathematical models of tumor-induced angiogenesis. Bull Math Biol. 1998;60:857–99. - PubMed
-
- Baish J, Gazit Y, Berk D, Nozue M, Baxter L, Jain R. Role of tumor vascular architecture in nutrient and drug delivery: an invasion percolation-based network model. Microvasc Res. 1996;51:327–46. - PubMed
-
- Baish J, Jain R. Fractals and cancer. Cancer Res. 2000;60:3683–8. - PubMed
-
- Basciano C, Kleinstreuer C, Kennedy A, Dezarn W, Childress E. Computer modeling of controlled microsphere release and targeting in a representative hepatic artery system. Ann Biomed Eng. 2010;38:1862–79. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous
