Bayesian methods for multivariate modeling of pleiotropic SNP associations and genetic risk prediction
- PMID: 22973300
- PMCID: PMC3438684
- DOI: 10.3389/fgene.2012.00176
Bayesian methods for multivariate modeling of pleiotropic SNP associations and genetic risk prediction
Abstract
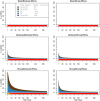
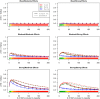
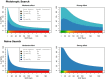
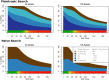
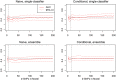
Genome-wide association studies (GWAS) have identified numerous associations between genetic loci and individual phenotypes; however, relatively few GWAS have attempted to detect pleiotropic associations, in which loci are simultaneously associated with multiple distinct phenotypes. We show that pleiotropic associations can be directly modeled via the construction of simple Bayesian networks, and that these models can be applied to produce single or ensembles of Bayesian classifiers that leverage pleiotropy to improve genetic risk prediction. The proposed method includes two phases: (1) Bayesian model comparison, to identify Single-Nucleotide Polymorphisms (SNPs) associated with one or more traits; and (2) cross-validation feature selection, in which a final set of SNPs is selected to optimize prediction. To demonstrate the capabilities and limitations of the method, a total of 1600 case-control GWAS datasets with two dichotomous phenotypes were simulated under 16 scenarios, varying the association strengths of causal SNPs, the size of the discovery sets, the balance between cases and controls, and the number of pleiotropic causal SNPs. Across the 16 scenarios, prediction accuracy varied from 90 to 50%. In the 14 scenarios that included pleiotropically associated SNPs, the pleiotropic model search and prediction methods consistently outperformed the naive model search and prediction. In the two scenarios in which there were no true pleiotropic SNPs, the differences between the pleiotropic and naive model searches were minimal. To further evaluate the method on real data, a discovery set of 1071 sickle cell disease (SCD) patients was used to search for pleiotropic associations between cerebral vascular accidents and fetal hemoglobin level. Classification was performed on a smaller validation set of 352 SCD patients, and showed that the inclusion of pleiotropic SNPs may slightly improve prediction, although the difference was not statistically significant. The proposed method is robust, computationally efficient, and provides a powerful new approach for detecting and modeling pleiotropic disease loci.
Keywords: Bayesian; GWAS; SNP; pleiotropy; prediction.
Figures
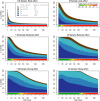
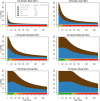
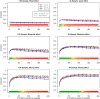
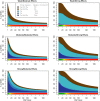


References
-
- Gupta M., Cheung C. L., Hsu Y. H., Demissie S., Cupples L. A., Kiel D. P., Karasik D. (2011). Identification of homogenous genetic architecture of multiple genetically correlated traits by block clustering of genome-wide associations. J. Bone Miner. Res. 26, 1261–127110.1002/jbmr.333 - DOI - PMC - PubMed
-
- Hand D. J. (2009). “Naive Bayes,” in The Top Ten Algorithms in Data Mining, eds Wu X., Kumar V. (London: Chapman and Hall; ), 163–178
Grants and funding
LinkOut - more resources
Full Text Sources

