Efficient universal computing architectures for decoding neural activity

Abstract

The ability to decode neural activity into meaningful control signals for prosthetic devices is critical to the development of clinically useful brain- machine interfaces (BMIs). Such systems require input from tens to hundreds of brain-implanted recording electrodes in order to deliver robust and accurate performance; in serving that primary function they should also minimize power dissipation in order to avoid damaging neural tissue; and they should transmit data wirelessly in order to minimize the risk of infection associated with chronic, transcutaneous implants. Electronic architectures for brain- machine interfaces must therefore minimize size and power consumption, while maximizing the ability to compress data to be transmitted over limited-bandwidth wireless channels. Here we present a system of extremely low computational complexity, designed for real-time decoding of neural signals, and suited for highly scalable implantable systems. Our programmable architecture is an explicit implementation of a universal computing machine emulating the dynamics of a network of integrate-and-fire neurons; it requires no arithmetic operations except for counting, and decodes neural signals using only computationally inexpensive logic operations. The simplicity of this architecture does not compromise its ability to compress raw neural data by factors greater than [Formula: see text]. We describe a set of decoding algorithms based on this computational architecture, one designed to operate within an implanted system, minimizing its power consumption and data transmission bandwidth; and a complementary set of algorithms for learning, programming the decoder, and postprocessing the decoded output, designed to operate in an external, nonimplanted unit. The implementation of the implantable portion is estimated to require fewer than 5000 operations per second. A proof-of-concept, 32-channel field-programmable gate array (FPGA) implementation of this portion is consequently energy efficient. We validate the performance of our overall system by decoding electrophysiologic data from a behaving rodent.

Figure 1. Universal Computing Architecture for Neural Decoding.

The overall architecture of a neural decoding system is decomposed into a set of operations implemented by Turing-type computing machines, shown here as a collection of heads (data processing units) reading from and writing to a set of corresponding tapes (programs and data streams). Amplification and digitization of raw neural data, and decoding of that data, are performed by heads N and I, respectively, in a biologically implanted unit. The ‘Internal Computations’ of these two system components are streamed across a wireless data channel to an external unit, which performs more power-intensive ‘External Computations’ to post-process the decoded output. Further processing of the decoded data is performed externally by head E, and the final output of the system is reported by head O. The external system implements a learning algorithm that is used to write the program on the threshold tape, which is executed by the internal unit.

Figure 2. Decoding Architecture.

Block diagram of the low-power processing system of the internal component of our neural decoder, as implemented in one instantiation of our architecture. Functional blocks are color-coded in accord with the scheme used in Figure 1.

Figure 3. Encoding of Position by Place Cell Receptive Fields.

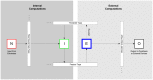
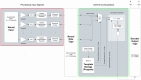
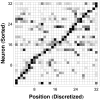
Normalized spike rate for each of neurons in equal-length intervals along a one-dimensional track maze. Neurons (rows) have been sorted according to their positions of maximal activity to illustrate that the receptive fields of the place cells in this population cover the one-dimensional space of interest. Neuronal spike rates for each cell in each state (row elements) have been normalized to the highest spike rate (maximal row element) exhibited by the particular cell over all states. (Black: Maximal Spike Rate, White: Zero Spike Rate, Gray: Intermediate Spike Rates.).

Figure 4. Decoder Logic Program: Finite-State Automaton Rules for Neural Decoding.

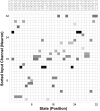
Decoding template array stored in system memory, resulting in the output shown in Figure 5, using the most informative threshold values for each position state. Some elements of the rule table (three pair) are empty, with corresponding columns having fewer than nonwhite elements, because the associated states had fewer than channels able to satisfy and , the minimum sensitivity and positive predictive value, respectively, for state decoding. (White: Unused, Light Gray: Spike per -ms Window, Black: Spikes per -ms Window.) Intuitively, this set of templates can be understood as the tape-reading rules for a Turing machine, whose symbols are generated by the time-windowed spike counts on neural input channels, and whose states correspond to a discretized set of position states encoded by the underlying neuronal populations. At each time step, the neural decoder scans down each column in the array to determine the states, if any, whose rules have been satisfied; the decoded output elements are set to for those states, and to otherwise. The rules displayed graphically in the rectangular array are encoded numerically in the table displayed above the array (which is reproduced in Table 1). The columns of the table are aligned with the states in the array for which they contain decoding data, comprising the indices of the two most informative channels, and , and the corresponding spike thresholds, and .

Figure 5. Decoder Output when Decoding Position from Hippocampal Place Cells.

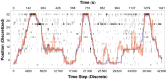
Our system decodes the location of a maze-roaming rat, from spike trains recorded from thirty-two hippocampal place cells. Raw output of the decoding algorithm, , is shown as a raster array, with the output at each time step displayed as a vertical column of pixels (black pixels correspond to , white pixels to ). Red lines show the trajectories obtained after applying our Viterbi algorithm to the raw decoder output, as described in the text. The actual trajectories of the rat are shown in blue. Decoding accuracy and decoder noise are affected by the length of the time window over which spikes are collected at each time step: ms ( ms). Here the decoded trajectory matches the actual trajectory with a correlation coefficient of .

Figure 6. Histograms and Threshold.

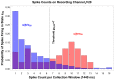
Histograms collected during the training phase of the decoding algorithm facilitate computation of thresholds for windowed spike activity, which are stored as templates in memory and used to discriminate between states. This histogram of spike activity, collected from recording channel , demonstrates that a threshold of spikes per -ms window, on recording channel , is sensitive and specific for state (Sensitivity: , Specificity: , Positive Predictive Value: ). This threshold is written on the threshold tape used to program the internal unit of the decoder, and can be seen numerically in Figure 4 as the and row entries of column , and graphically as the corresponding pixels in the rule array.