Describing small-scale structure in random media using pulse-echo ultrasound

Abstract

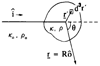
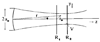
A method for estimating structural properties of random media is described. The size, number density, and scattering strength of particles are estimated from an analysis of the radio frequency (rf) echo signal power spectrum. Simple correlation functions and the accurate scattering theory of Faran [J.J. Faran, J. Acoust. Soc. Am. 23, 405-418 (1951)], which includes the effects of shear waves, were used separately to model backscatter from spherical particles and thereby describe the structures of the medium. These methods were tested using both glass sphere-in-agar and polystyrene sphere-in-agar scattering media. With the appropriate correlation function, it was possible to measure glass sphere diameters with an accuracy of 20%. It was not possible to accurately estimate the size of polystyrene spheres with the simple spherical and Gaussian correlation models examined because of a significant shear wave contribution. Using the Faran scattering theory for spheres, however, the accuracy for estimating diameters was improved to 10% for both glass and polystyrene scattering media. It was possible to estimate the product of the average scattering particle number density and the average scattering strength per particle, but with lower accuracy than the size estimates. The dependence of the measurement accuracy on the inclusion of shear waves, the wavelength of sound, and medium attenuation are considered, and the implications for describing the structure of biological soft tissues are discussed.

FIG. 1

Scattering geometry illustration showing a point r′ inside the scattering volume.

FIG. 2

(a) Form factors for the fluid sphere model F₁, the spherical shell model F₂, and the Gaussian model F₃; F₄ and F₆ are form factors calculated from the Faran scattering theory for microspheres made of glass and fat, respectively. (b) Form factor for the rigid, immovable sphere F_r is plotted along with the fluid sphere model F₁ (solid lines) and that calculated for glass, polystyrene, and fat microspheres from the Faran scattering theory. These data include the effects of shear waves generated inside the particle. (c) Same as (b), except that the glass, polystyrene, and fat data are calculated from the theory of Morse and Ingard. These results do not include the effects of shear waves. (d) Form factors for collagen along and across the fibers. The results are computed using the Faran theory and the parameters are taken from the work of Cusak and Miller. These results show that scattering from collagen spheres may be approximated by that of polystyrene.

FIG. 3

Transducer geometry in the y,z plane.

FIG. 4

Measured (noisy line) and modeled (smooth line) form factors for a 105-µm-diam glass microsphere sample (Table I) scanned using a 5-MHz broadband transducer (Table II). The spherical shell model F₂ with a 95-µm-diam sphere size gave the best fit (MASD) to the data over the transducer bandwidth.

FIG. 5

Comparison between form factors measured for the 81-µm polystyrene microsphere sample (noisy lines) and modeled using the scattering theory of Faran and assuming 83-µm-diam spheres (smooth line). Three transducers were used to span the range of 1.5–9.5 MHz as indicated. A 2.25-MHz transducer was used to obtain data from 1.5 to 3.2 MHz, a 5.0-MHz transducer from 2.8 to 6.5 MHz, and a 7.5-MHz transducer from 5.5 to 9.5 MHz. The three data segments were scaled individually to give the appearance of a continuous line. No modifications to the frequency dependence of the data were made.

FIG. 6

Plots of the variation in particle size estimates with an uncertainty in the linear attenuation slope estimate. The results depend on the value of ka, and span the range of attenuation values typical in soft biological tissues. The errors for ka = 1.22 and ka = 1.07 are identical. Lower values of ka give rise to larger errors.