Combining boundary-based methods with tensor-based morphometry in the measurement of longitudinal brain change
- PMID: 23014714
- PMCID: PMC3775845
- DOI: 10.1109/TMI.2012.2220153
Combining boundary-based methods with tensor-based morphometry in the measurement of longitudinal brain change
Abstract
Tensor-based morphometry is a powerful tool for automatically computing longitudinal change in brain structure. Because of bias in images and in the algorithm itself, however, a penalty term and inverse consistency are needed to control the over-reporting of nonbiological change. These may force a tradeoff between the intrinsic sensitivity and specificity, potentially leading to an under-reporting of authentic biological change with time. We propose a new method incorporating prior information about tissue boundaries (where biological change is likely to exist) that aims to keep the robustness and specificity contributed by the penalty term and inverse consistency while maintaining localization and sensitivity. Results indicate that this method has improved sensitivity without increased noise. Thus it will have enhanced power to detect differences within normal aging and along the spectrum of cognitive impairment.
Figures
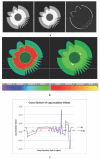
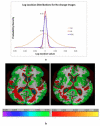
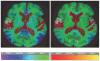
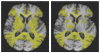
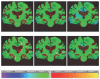
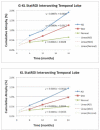
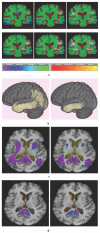
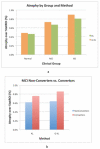
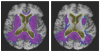
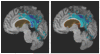
Similar articles
-
Longitudinal image registration with non-uniform appearance change.Med Image Comput Comput Assist Interv. 2012;15(Pt 3):280-8. doi: 10.1007/978-3-642-33454-2_35. Med Image Comput Comput Assist Interv. 2012. PMID: 23286141 Free PMC article.
-
Comparing registration methods for mapping brain change using tensor-based morphometry.Med Image Anal. 2009 Oct;13(5):679-700. doi: 10.1016/j.media.2009.06.002. Epub 2009 Jun 24. Med Image Anal. 2009. PMID: 19631572 Free PMC article.
-
CLASSIC: consistent longitudinal alignment and segmentation for serial image computing.Inf Process Med Imaging. 2005;19:101-13. doi: 10.1007/11505730_9. Inf Process Med Imaging. 2005. PMID: 17354688
-
Nonlinear registration of diffusion MR images based on fiber bundles.Med Image Comput Comput Assist Interv. 2007;10(Pt 1):351-8. doi: 10.1007/978-3-540-75757-3_43. Med Image Comput Comput Assist Interv. 2007. PMID: 18051078
-
Computational anatomy with the SPM software.Magn Reson Imaging. 2009 Oct;27(8):1163-74. doi: 10.1016/j.mri.2009.01.006. Epub 2009 Feb 27. Magn Reson Imaging. 2009. PMID: 19249168 Review.
Cited by
-
Comparison of Education and Episodic Memory as Modifiers of Brain Atrophy Effects on Cognitive Decline: Implications for Measuring Cognitive Reserve.J Int Neuropsychol Soc. 2021 May;27(5):401-411. doi: 10.1017/S1355617720001095. Epub 2021 Jan 18. J Int Neuropsychol Soc. 2021. PMID: 33455611 Free PMC article.
-
A robust brain signature region approach for episodic memory performance in older adults.Brain. 2021 May 7;144(4):1089-1102. doi: 10.1093/brain/awab007. Brain. 2021. PMID: 33895818 Free PMC article.
-
Growth-Associated Protein 43 and Tensor-Based Morphometry Indices in Mild Cognitive Impairment.Neuroinformatics. 2024 Jul;22(3):239-250. doi: 10.1007/s12021-024-09663-9. Epub 2024 Apr 17. Neuroinformatics. 2024. PMID: 38630411
-
Dynamic change of cognitive reserve: associations with changes in brain, cognition, and diagnosis.Neurobiol Aging. 2019 Nov;83:95-104. doi: 10.1016/j.neurobiolaging.2019.08.016. Epub 2019 Aug 21. Neurobiol Aging. 2019. PMID: 31585371 Free PMC article.
-
Ethnoracial differences in brain structure change and cognitive change.Neuropsychology. 2018 Jul;32(5):529-540. doi: 10.1037/neu0000452. Epub 2018 Apr 12. Neuropsychology. 2018. PMID: 29648842 Free PMC article.
References
-
- Sharma S, et al. Use of simulated atrophy for performance analysis of brain atrophy estimation approaches; Proc. MICCAI 2009; 2009.pp. 566–574. - PubMed
-
- Freeborough P, Fox N. The boundary shift integral: An accurate and robust measure of cerebral volume change from registered repeat MRI. IEEE Trans. Med. Imaging. 1997 Oct;16(5):623–629. - PubMed
-
- Leow AD, et al. Statistical properties of Jacobian maps and the realization of unbiased large-deformation nonlinear image registration. IEEE Trans. Med. Imag. 2007;26:822–832. - PubMed
-
- Yanovsky I, et al. Topology preserving log-unbiased nonlinear image registration: Theory and implementation; IEEE Conf. Comput. Vis. Pattern Recognit.; Minneapolois, MN. 2007.pp. 1–8.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

