Risk-sensitivity in Bayesian sensorimotor integration
- PMID: 23028294
- PMCID: PMC3459842
- DOI: 10.1371/journal.pcbi.1002698
Risk-sensitivity in Bayesian sensorimotor integration
Abstract
Information processing in the nervous system during sensorimotor tasks with inherent uncertainty has been shown to be consistent with Bayesian integration. Bayes optimal decision-makers are, however, risk-neutral in the sense that they weigh all possibilities based on prior expectation and sensory evidence when they choose the action with highest expected value. In contrast, risk-sensitive decision-makers are sensitive to model uncertainty and bias their decision-making processes when they do inference over unobserved variables. In particular, they allow deviations from their probabilistic model in cases where this model makes imprecise predictions. Here we test for risk-sensitivity in a sensorimotor integration task where subjects exhibit Bayesian information integration when they infer the position of a target from noisy sensory feedback. When introducing a cost associated with subjects' response, we found that subjects exhibited a characteristic bias towards low cost responses when their uncertainty was high. This result is in accordance with risk-sensitive decision-making processes that allow for deviations from Bayes optimal decision-making in the face of uncertainty. Our results suggest that both Bayesian integration and risk-sensitivity are important factors to understand sensorimotor integration in a quantitative fashion.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
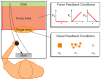
 ,
,  or
or  . Furthermore, we imposed three different force functions (
. Furthermore, we imposed three different force functions ( ,
,  and
and  ) in the force area, where the force depended on the presumed target position as they indicated it by their forward movement. Screenshots of the actual display can be found in Text S1.
) in the force area, where the force depended on the presumed target position as they indicated it by their forward movement. Screenshots of the actual display can be found in Text S1.
 ,
,  and
and  ). Each panel compares the three different force conditions
). Each panel compares the three different force conditions  (red),
(red),  (green) and
(green) and  (blue). The model predicts that higher levels of uncertainty are associated with higher slopes and that higher forces are associated with shifts in the intercept that are proportional to the uncertainty.
(blue). The model predicts that higher levels of uncertainty are associated with higher slopes and that higher forces are associated with shifts in the intercept that are proportional to the uncertainty.
 ,
,  and
and  . The three different feedback conditions
. The three different feedback conditions  ,
,  and
and  are displayed within each panel. It can be seen that the slope increases with increasing uncertainty. The intercepts are modulated by both uncertainty and force condition.
are displayed within each panel. It can be seen that the slope increases with increasing uncertainty. The intercepts are modulated by both uncertainty and force condition.References
-
- Doya K, Ishii S, Pouget A, Rao RPN, editors (2007) Bayesian Brain: Probabilistic Approaches to Neural Coding. Boston: MIT Press.
-
- Knill DC, Pouget A (2004) The bayesian brain: the role of uncertainty in neural coding and computation. Trends Neurosci 27: 712–719. - PubMed
-
- Körding KP, Wolpert DM (2004) Bayesian integration in sensorimotor learning. Nature 427: 244–247. - PubMed
-
- Körding KP, Wolpert DM (2006) Bayesian decision theory in sensorimotor control. Trends Cogn Sci 10: 319–326. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

