Time-delayed mutual information of the phase as a measure of functional connectivity
- PMID: 23028571
- PMCID: PMC3445535
- DOI: 10.1371/journal.pone.0044633
Time-delayed mutual information of the phase as a measure of functional connectivity
Abstract
We propose a time-delayed mutual information of the phase for detecting nonlinear synchronization in electrophysiological data such as MEG. Palus already introduced the mutual information as a measure of synchronization. To obtain estimates on small data-sets as reliably as possible, we adopt the numerical implementation as proposed by Kraskov and colleagues. An embedding with a parametric time-delay allows a reconstruction of arbitrary nonstationary connective structures--so-called connectivity patterns--in a wide class of systems such as coupled oscillatory or even purely stochastic driven processes. By using this method we do not need to make any assumptions about coupling directions, delay times, temporal dynamics, nonlinearities or underlying mechanisms. For verifying and refining the methods we generate synthetic data-sets by a mutual amplitude coupled network of Rössler oscillators with an a-priori known connective structure. This network is modified in such a way, that the power-spectrum forms a 1/f power law, which is also observed in electrophysiological recordings. The functional connectivity measure is tested on robustness to additive uncorrelated noise and in discrimination of linear mixed input data. For the latter issue a suitable de-correlation technique is applied. Furthermore, the compatibility to inverse methods for a source reconstruction in MEG such as beamforming techniques is controlled by dedicated dipole simulations. Finally, the method is applied on an experimental MEG recording.
Conflict of interest statement
Figures

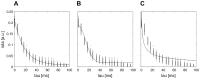
 as the input of Eq.(5) for modeling a connective structure. The pattern on the left is given by a Gaussian in the
as the input of Eq.(5) for modeling a connective structure. The pattern on the left is given by a Gaussian in the  -plane centred at
-plane centred at  ms and
ms and  ms. The pattern on the right includes an additional spurious non-zero background activation (right), which is generated by Gaussian filtered Poisson noise and decays for high time-delays. B Simulated time-series
ms. The pattern on the right includes an additional spurious non-zero background activation (right), which is generated by Gaussian filtered Poisson noise and decays for high time-delays. B Simulated time-series  with oscillatory (left) and a more stochastic (right) behavior. The maximum of the connectivity is shown via dashed lines: black indicates the driving system and grey the driven system. A comparison of the corresponding power-spectra
with oscillatory (left) and a more stochastic (right) behavior. The maximum of the connectivity is shown via dashed lines: black indicates the driving system and grey the driven system. A comparison of the corresponding power-spectra  points out a
points out a  characteristic (dotted black line) for the system including a spurious background synchronization (dashed black line), which can be also observed in MEG recordings (grey line). C Corresponding mutual phase information
characteristic (dotted black line) for the system including a spurious background synchronization (dashed black line), which can be also observed in MEG recordings (grey line). C Corresponding mutual phase information  for
for  trials. A high connectivity is indicated by a high mutual information. The system featuring a background synchronicity (right) holds a damped, less extended and weaker connectivity in the
trials. A high connectivity is indicated by a high mutual information. The system featuring a background synchronicity (right) holds a damped, less extended and weaker connectivity in the  -plane.
-plane.
 trials with a
trials with a  spectrum, cf. Methods (A modified Rössler network). A
spectrum, cf. Methods (A modified Rössler network). A
 of two mixed sources. Each pattern represents a connection directed from
of two mixed sources. Each pattern represents a connection directed from  (upper) and
(upper) and  (lower part). A sliding window
(lower part). A sliding window  ms is applied for the estimation. The dashed line indicates the modeled connectivity, cf. Fig. 1A. Parameter
ms is applied for the estimation. The dashed line indicates the modeled connectivity, cf. Fig. 1A. Parameter  sets the mixing strength as referred to Eq. (7). In B the pattern is de-correlated by subtracting Eq. (8), which is fitted in the pre-stimulus interval from
sets the mixing strength as referred to Eq. (7). In B the pattern is de-correlated by subtracting Eq. (8), which is fitted in the pre-stimulus interval from  ms to 0 ms. The
ms to 0 ms. The  is computed on a triangular grid with a distance of
is computed on a triangular grid with a distance of  between neighbored estimates. Significant increased synchronization is indicated by a white dot on the grid using a FDR with
between neighbored estimates. Significant increased synchronization is indicated by a white dot on the grid using a FDR with  .
.
 and an additive noise level of 100 RMS).
and an additive noise level of 100 RMS).
 of the de-mixed sources are shown. The same data-set is used as in Fig. 2A. The computation and statistical validation of
of the de-mixed sources are shown. The same data-set is used as in Fig. 2A. The computation and statistical validation of  are performed analogously to the results of Fig. 2A.
are performed analogously to the results of Fig. 2A.
 for a variate number of trials
for a variate number of trials  . A Two uncorrelated and b) two strongly correlated and noisy sources. The same de-correlation step is applied as in Fig. 2B. The same data-set is used as given in Fig. 2. The black dashed line indicates the center of the modeled connectivity.
. A Two uncorrelated and b) two strongly correlated and noisy sources. The same de-correlation step is applied as in Fig. 2B. The same data-set is used as given in Fig. 2. The black dashed line indicates the center of the modeled connectivity.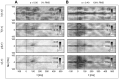
 and without additive uncorrelated white noise, B strong correlated sources with
and without additive uncorrelated white noise, B strong correlated sources with  and high additive uncorrelated white noise with
and high additive uncorrelated white noise with  .
.  denotes the absolute value of the cross-correlation of the amplitude.
denotes the absolute value of the cross-correlation of the amplitude.  is the phase coherence in time-domain, cf. Eq. (9) with
is the phase coherence in time-domain, cf. Eq. (9) with  ,
,  the phase synchronization based on the Shannon-entropy, cf. Eq. (10) with
the phase synchronization based on the Shannon-entropy, cf. Eq. (10) with  , and
, and  the mutual information of the phase, cf. Eq. (4). The same data-set with
the mutual information of the phase, cf. Eq. (4). The same data-set with  trials is used as shown in Fig. 2A. The connectivity patterns are estimated with a moving time window
trials is used as shown in Fig. 2A. The connectivity patterns are estimated with a moving time window  ms and de-correlated analogously to Fig. 2B. The temporal coordinate of the underlying connectivity is indicated by a black dashed line. Because
ms and de-correlated analogously to Fig. 2B. The temporal coordinate of the underlying connectivity is indicated by a black dashed line. Because  ,
,  and
and  are estimated in every bin, the significant increased correlation is indicated by a white area (FDR with
are estimated in every bin, the significant increased correlation is indicated by a white area (FDR with  ).
).
 of the input data. Modified Rössler system with a
of the input data. Modified Rössler system with a  spectrum is used as time-course of three sequentially chained dipoles, cf. Table 1 and 2.
spectrum is used as time-course of three sequentially chained dipoles, cf. Table 1 and 2.  trials were simulated with an additive uncorrelated sensor noise of
trials were simulated with an additive uncorrelated sensor noise of  RMS. Brain noise is adapted by
RMS. Brain noise is adapted by  uncorrelated, randomly located and orientated dipoles in the grey matter. B Connectivity of the reconstructed source activation with a conventional LCMV beamforming method. C Reconstructed connectivity by applying a weighted LCMV in a preprocessing step: data in sensor space is filtered by a linear weighted moving average in order to suppress thermal noise of the MEG device. The smoothed signals are mapped onto the cortex and the functional connectivity among the reconstructed source activation is estimated. In B and C patterns are unprocessed (left) and processed by an de-correlation on pattern level (right) as suggested in the Results (Pattern de-correlation).
uncorrelated, randomly located and orientated dipoles in the grey matter. B Connectivity of the reconstructed source activation with a conventional LCMV beamforming method. C Reconstructed connectivity by applying a weighted LCMV in a preprocessing step: data in sensor space is filtered by a linear weighted moving average in order to suppress thermal noise of the MEG device. The smoothed signals are mapped onto the cortex and the functional connectivity among the reconstructed source activation is estimated. In B and C patterns are unprocessed (left) and processed by an de-correlation on pattern level (right) as suggested in the Results (Pattern de-correlation).
 of the input data (
of the input data ( trials of a Rössler system), cf. Table 1 and 2. B Connectivity of the reconstructed source activation with a conventional LCMV beamforming. C Reconstructed connectivity by applying a WMA filter on sensor data in a preprocessing step (WMA+LCMV). In B and C the patterns are unprocessed (left) and de-correlated (right) as suggested in the Resutls (Pattern de-correlation). Significant improvements in the connectivity reconstruction compared to the patterns of the conventional beamformer without de-correlation are marked by white solid circles.
trials of a Rössler system), cf. Table 1 and 2. B Connectivity of the reconstructed source activation with a conventional LCMV beamforming. C Reconstructed connectivity by applying a WMA filter on sensor data in a preprocessing step (WMA+LCMV). In B and C the patterns are unprocessed (left) and de-correlated (right) as suggested in the Resutls (Pattern de-correlation). Significant improvements in the connectivity reconstruction compared to the patterns of the conventional beamformer without de-correlation are marked by white solid circles.
 uncorrelated, randomly located and orientated dipoles in the grey matter. A Connectivity
uncorrelated, randomly located and orientated dipoles in the grey matter. A Connectivity  of the connected Rössler oscillators indexed with
of the connected Rössler oscillators indexed with  and
and  , cf. Table 1 and 2. B Connectivity of the reconstructed source activation with a conventional LCMV beamforming approach. C Reconstructed connectivity by applying a WMA filter to reduce thermal noise captured by the MEG device on sensor data (WMA+LCMV). All patterns in b) and c) are processed by removing exponentially decaying correlations as described in the Results (Pattern de-correlation).
, cf. Table 1 and 2. B Connectivity of the reconstructed source activation with a conventional LCMV beamforming approach. C Reconstructed connectivity by applying a WMA filter to reduce thermal noise captured by the MEG device on sensor data (WMA+LCMV). All patterns in b) and c) are processed by removing exponentially decaying correlations as described in the Results (Pattern de-correlation).
 for 3–150 Hz in terms of the functional connectivity between a temporal and frontal cortical area during a passive viewing of faces with neutral expression. The interval
for 3–150 Hz in terms of the functional connectivity between a temporal and frontal cortical area during a passive viewing of faces with neutral expression. The interval  –0 ms was taken to estimate a statistical threshold with a FDR ratio of
–0 ms was taken to estimate a statistical threshold with a FDR ratio of  . Significant changes are marked by white dots. The patterns were de-correlated with
. Significant changes are marked by white dots. The patterns were de-correlated with  . The rows are given by a Negative conditioning with
. The rows are given by a Negative conditioning with  and a Neutral control with
and a Neutral control with  . In the contrast Negative-Neutral the processing of faces is compensated by subtracting the Neutral baseline. The columns denote connectivity before conditioning (Pre), after conditioning (Post) and the contrast Post-Pre, which shows the change in connectivity through the conditioning process. Cluster locations are calculated by the center of gravity and marked by cross hairs. Numerical values of the location are listed in Table 3.
. In the contrast Negative-Neutral the processing of faces is compensated by subtracting the Neutral baseline. The columns denote connectivity before conditioning (Pre), after conditioning (Post) and the contrast Post-Pre, which shows the change in connectivity through the conditioning process. Cluster locations are calculated by the center of gravity and marked by cross hairs. Numerical values of the location are listed in Table 3.
 , Gaussian with
, Gaussian with  and Power law with
and Power law with  . Data from the interval
. Data from the interval  –0 ms provides a baseline for the FDR threshold in Pre-Stimulus. As an alternative approach Surrogate data was estimated by destroying correlation in phases. Significant higher connectivities are marked by white dots.
–0 ms provides a baseline for the FDR threshold in Pre-Stimulus. As an alternative approach Surrogate data was estimated by destroying correlation in phases. Significant higher connectivities are marked by white dots.Similar articles
-
The impact of MEG source reconstruction method on source-space connectivity estimation: A comparison between minimum-norm solution and beamforming.Neuroimage. 2017 Aug 1;156:29-42. doi: 10.1016/j.neuroimage.2017.04.038. Epub 2017 May 4. Neuroimage. 2017. PMID: 28479475
-
A method for the estimation of functional brain connectivity from time-series data.Cogn Neurodyn. 2010 Jun;4(2):133-49. doi: 10.1007/s11571-010-9107-z. Epub 2010 Mar 6. Cogn Neurodyn. 2010. PMID: 21629586 Free PMC article.
-
Phase shift invariant imaging of coherent sources (PSIICOS) from MEG data.Neuroimage. 2018 Dec;183:950-971. doi: 10.1016/j.neuroimage.2018.08.031. Epub 2018 Aug 22. Neuroimage. 2018. PMID: 30142449
-
Electrophysiological Source Imaging: A Noninvasive Window to Brain Dynamics.Annu Rev Biomed Eng. 2018 Jun 4;20:171-196. doi: 10.1146/annurev-bioeng-062117-120853. Epub 2018 Mar 1. Annu Rev Biomed Eng. 2018. PMID: 29494213 Free PMC article. Review.
-
Review of advanced techniques for the estimation of brain connectivity measured with EEG/MEG.Comput Biol Med. 2011 Dec;41(12):1110-7. doi: 10.1016/j.compbiomed.2011.06.020. Epub 2011 Jul 26. Comput Biol Med. 2011. PMID: 21794851 Review.
Cited by
-
Probing Asymmetric Interactions with Time-Separated Mutual Information: A Case Study Using Golden Shiners.Entropy (Basel). 2024 Sep 10;26(9):775. doi: 10.3390/e26090775. Entropy (Basel). 2024. PMID: 39330108 Free PMC article.
-
Connectivity Analysis for Multivariate Time Series: Correlation vs. Causality.Entropy (Basel). 2021 Nov 25;23(12):1570. doi: 10.3390/e23121570. Entropy (Basel). 2021. PMID: 34945876 Free PMC article.
-
Event-Marked Windowed Communication: Inferring Activity Propagation from Neural Time Series.Hum Brain Mapp. 2025 Jun 1;46(8):e70223. doi: 10.1002/hbm.70223. Hum Brain Mapp. 2025. PMID: 40444898 Free PMC article.
-
Distinct roles of delta- and theta-band neural tracking for sharpening and predictive coding of multi-level speech features during spoken language processing.Hum Brain Mapp. 2023 Dec 1;44(17):6149-6172. doi: 10.1002/hbm.26503. Epub 2023 Oct 11. Hum Brain Mapp. 2023. PMID: 37818940 Free PMC article.
-
The characterization of hippocampal theta-driving neurons - a time-delayed mutual information approach.Sci Rep. 2017 Jul 17;7(1):5637. doi: 10.1038/s41598-017-05527-2. Sci Rep. 2017. PMID: 28717183 Free PMC article.
References
-
- Palus M (1997) Detecting phase synchronization in noisy systems. Physics Letters A 235: 341–351.
-
- Kraskov A, Stogbauer H, Grassberger P (2004) Estimating mutual information. Phys Rev E Stat Nonlin Soft Matter Phys 69: 066138 1–16. - PubMed
-
- Pfurtscheller G, da Silva FHL (1999) Event-related EEG/MEG synchronization and desynchronization: basic principles. Clin Neurophysiol 110: 1842–1857. - PubMed
-
- Rodriguez E, George N, Lachaux JP, Martinerie J, Renault B, et al. (1999) Perception's shadow: long-distance synchronization of human brain activity. Nature 397: 430–433. - PubMed
MeSH terms
LinkOut - more resources
Full Text Sources

