Distinguishing between selective sweeps from standing variation and from a de novo mutation

Abstract

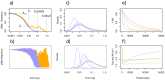
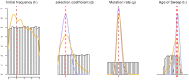
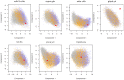
An outstanding question in human genetics has been the degree to which adaptation occurs from standing genetic variation or from de novo mutations. Here, we combine several common statistics used to detect selection in an Approximate Bayesian Computation (ABC) framework, with the goal of discriminating between models of selection and providing estimates of the age of selected alleles and the selection coefficients acting on them. We use simulations to assess the power and accuracy of our method and apply it to seven of the strongest sweeps currently known in humans. We identify two genes, ASPM and PSCA, that are most likely affected by selection on standing variation; and we find three genes, ADH1B, LCT, and EDAR, in which the adaptive alleles seem to have swept from a new mutation. We also confirm evidence of selection for one further gene, TRPV6. In one gene, G6PD, neither neutral models nor models of selective sweeps fit the data, presumably because this locus has been subject to balancing selection.

Figure 1. Characteristics of a selective sweep from standing variation.

orange: sweep from standing variation blue: sweep from a new mutation, blue: neutral model a: A cartoon of the allele frequency trajectory with relevant parameters: f ₁: allele frequency at the time selection started, f _cur: allele frequency at the time mutation is observed. t ₁: time at which selection started. t ₀: time when mutation arose.,. b: 100 stochastic realizations of the allele frequency trajectory. Panels c,d: Age distribution of an allele at 1% frequency and 5% frequency in a population (log scale). Blue line denotes neutrality, green lines represent selection with α = 20,100,200 and 1000 (right to left). Panels e,f: Distribution of the EHH (e) and H (f) statistic under neutrality (blue), a de novo mutation (green) and standing variation (red). Full and dashed lines represent selective pressures of α = 1,000 and 200, respectively. The dash-dot line represents α = 4000. Note that the slopes of the curves are different for the two scenarios, and the low H value around 0 under neutrality is due to the conditioning on a high frequency derived allele. Times are given in coalescent units and are plotted on a logarithmic scale.

Figure 2. Parameter estimation accuracy under SSV and SDN model.

Prior distributions are given as histograms; the orange and blue lines depict the average posterior distribution from 100 replicates of the parameters under the SSV and SDN model, respectively. The vertical dashed red line gives the parameters used for the simulation: α = 400, μ = 2.5e-8, f ₁ = 0.05, log(t ₁) = −1.51 (SSV)/−1.36(SDN). Estimates for the SSV model are less accurate for all parameters except μ, and 95% confidence intervals of estimates under the SSV model span the entire prior range for f ₁, α and t ₁. The age of the sweep is given in coalescence units.

Figure 3. Simulation results for ABC model choice procedure.

We simulated data using the fixed parameter values given in the lower part of the figure. The boxplots show the lower and upper quartiles, the median and the limits of a 95% interval of the posterior probability for the NT (blue), SSV (red) andSDN(green) models, respectively. Panel a: We compare the effect of the increasing selection coefficient α. Panel b: The effect of increasing initial frequency f ₁. Panel c: The effect of the current frequency f _cur, In panels a,b f _cur was set to 0.95, and in panel c, α = 1,000.

Figure 4. Parameter regions where distinction between models is possible.

On x and y axes are the prior ranges for selection coefficient and initial frequency of a selective sweep, respectively. Panels a, c and e give simulations under the SSV model, panels b, d and f for the SDN model. The different panels represent different current frequencies: In Panels a, b f _cur is 0.95, in c, d f _cur = 0.8 and in panels e and f f _cur = 0.5. Color gives the proportion of simulated data sets that were assigned to the correct model, when compared to the two alternative models. Black areas correspond to regions where this proportion is less than 50%, white areas to parameter regions where 95% or more of the data sets are correctly assigned. Each shade of grey corresponds to a 5% increase in the number of correctly assigned data sets.

Figure 5. Distribution of summary statistics of 7 genes.

This figure shows the observed (red) and prior predictive distribution of the first two PLS-DA components. Neutral simulations are shown in grey, SSV in orange and SDN in blue. For G6PD we show components 2 and 3 to highlight the finding that none of the three models analyzed is able to model the data for this gene.